Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bạn xem lại đề, AD đâu có bằng AB đâu mà góc AEB= góc ABD
+) Ta có: ^ACD = ^ACB + ^BCD; ^AEC = ^ABC + ^BAD
Mà ^ACB = ^ABC (∆ABC cân tại A); ^BCD = ^BAD (hai góc nội tiếp cùng chắn một cung)
nên ^ACD = ^AEC (1)
+) Dễ có: ∆AEB ~ ∆CED (g.g) nên \(\frac{AB}{CD}=\frac{AE}{CE}=\frac{AC}{CD}\)(2)
Từ (1) và (2), ta có: ^ACD = ^AEC và \(\frac{AE}{CE}=\frac{AC}{CD}\)nên ∆AEC ~ ACD (c.g.c)
\(\Rightarrow\frac{AC}{AD}=\frac{AE}{AC}\Rightarrow AC^2=AE.AD\)(đpcm)
vì AB =AC => sđ cung AB = sđ cung AC
=> 1/2 ( sđ CD + sđ AB ) =1/2 ( sđ CD + sđ AC )
=> AEB = 1/2 sđ AD =ABD
CM tam giác ABD ~ tam giác AEB ( g-g) => AC^2 = AD.AE
a)Xét (O) có:
góc PDA và góc PIA là 2 góc có đỉnh nằm trong đường tròn
=>góc PDA=\(\dfrac{sđ\stackrel\frown{AP}+sđ\stackrel\frown{BM}}{2}\),góc PIA=\(\dfrac{sđ\stackrel\frown{AP}+sđ\stackrel\frown{MC}}{2}\)
mà \(\stackrel\frown{BM}=\stackrel\frown{MC}\)(M là điểm chính giữa)
=> góc PDA = góc PIA
Xét tứ giác AIDP có
2 đỉnh D và I kề nhau cùng nhìn cạnh AP
góc PDA = góc PIA (cmt)
=>AIDP là tứ giác nội tiếp (dhnb)
b)Xét (O) có
PAB và PCB là 2 góc nội tiếp cùng chắn cung BP
=> góc PAB = góc PCB
mà góc PAB = góc PID ( tứ giác AIDP nội tiếp)
=> góc PCB= góc PID
=>ID//BC
c)CMTT câu trên ta được IE//BC
Mà ID//BC
=>IE trùng với ID(tiên đề ơ clit)
=> 3 ddierm D,I,E thẳng hàng
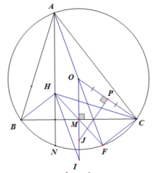
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)
