Cho đa thức f(x)= a4x4+a3x3+a2x2+a1x+a0
Biết rằng: f(1)=f(-1); f(2)=f(-2). Chứng minh: f(x)=f(-x) với mọi x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2017
Chọn D
Đạo hàm hai vế f(x)
Số hạng tổng quát thứ k + 1 trong khai triển thành đa thức của 
CM
22 tháng 4 2019
f(x) = anxn + an – 1xn– 1 + … + a1x + ao
+
g(x) = bnxn + bn – 1xn– 1 + … + b1x + bo
--------------------------------------------------------
f(x) + g(x) = (an + bn)xn + (an – 1 + bn – 1)xn– 1 + ….. + (a1 + b1)x + (ao + bo)
CM
6 tháng 8 2017
f(x) = anxn + an – 1xn– 1 + … + a1x + ao
-
g(x) = bnxn + bn – 1xn– 1 + … + b1x + bo
--------------------------------------------------------
f(x) - g(x) = (an - bn)xn + (an– 1 - bn – 1)xn– 1 + ..… + (a1 - b1)x + (ao - bo)
CM
25 tháng 12 2018
Chọn D.
Phương pháp:
Đạo hàm hàm số f(x) và chọn giá trị x phù hợp để tính giá trị biểu thức đề bài cho.
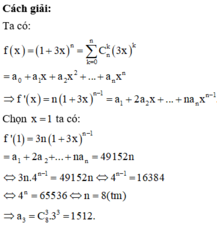
f(1) = f(-1)
=> a4 + a3 + a2 + a1 + a0 = a4 - a3 + a2 - a1 + a0
=> a3 + a1 = - a3 - a1
=> a3 = a1 = 0 hoặc a3 = -a1 (1)
f(2) = f(-2)
=> 16a4 + 8a3 + 4a2 + 2a1 + a0 = 16a4 - 8a3 + 4a2 - 2a1 + a0
=> 8a3 + 2a1 = - 8a3 - 2a1
=> a3 = a1 = 0 hoặc 4a3 = -a1 (2)
(1) và (2) => a3 = a1 = 0
=> f(x) = a4x4 + a2x2+ a0
x4 và x2 là số mũ chẵn
=> x4 = (-x)4 và x2 = (-x)2
=> f(x) = f(-x) với mọi x
Theo mình biết thì cái này là hàm số chẵn.