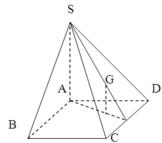
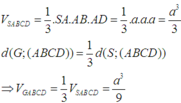Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
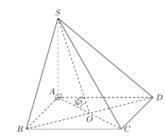
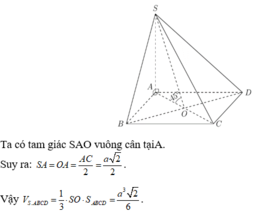
Ta có tam giác SAO vuông cân tạiA.
Suy ra:
S
A
=
O
A
=
A
C
2
=
a
2
2
Vậy : V S . A B C D = 1 3 . S O . S A B C D = a 3 2 6

Đáp án C
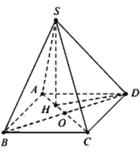
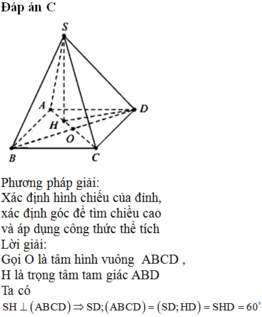
Phương pháp giải:
Xác định hình chiếu của đỉnh, xác định góc để tìm chiều cao và áp dụng công thức thể tích
Lời giải:
Gọi O là tâm hình vuông ABCD , H là trọng tâm tam giác ABD
Ta có ![]()
![]()
ABCD là hình vuông cạnh a nên 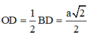
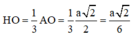
Tam giác HDO vuông tại O, có 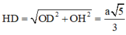
Tam giác SHD vuông tại H, có 
Vậy thể tích cần tính là 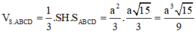

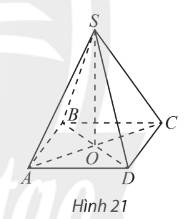
Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)

a: (SAB) giao (ABCD)=AB
SA vuông góc AB, SA thuộc (SAB)
AD vuông góc AB, AD thuộc (ABCD)
=>((SAB);(ABCD))=góc SAD=90 độ