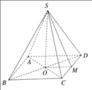
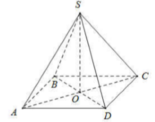
Cho hình chóp tứ giác đều S.ABCD biết đường cao SO = 12 cm; cạnh đáy CD = 6,5 cm. Tính thể tích hình chóp tứ giác đều S.ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

14 tháng 6 2021
a) Áp dụng định lý Pytago, ta được:
AC2=AB2+BC2=2AB2AC2=AB2+BC2=2AB2
⇒AC=AB√2=10√2cm⇒AC=AB2=102cm
b) Gọi MM là trung điểm ABAB
⇒MA=MB=MO=5cm⇒MA=MB=MO=5cm
⇒SM⊥AB⇒SM⊥AB (ΔSAB∆SAB cân tại SS)
⇒SM=√SA2−AM2=√122−52=√119cm⇒SM=SA2−AM2=122−52=119cm
⇒SO=√SM2−OM2=√119−52=√94cm⇒SO=SM2−OM2=119−52=94cm
⇒VS.ABCD=13.SABCD.SO=13.AB2.SO=102.943=94003cm3

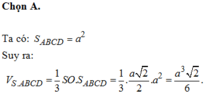




Diện tích mặt đáy của chóp tứ giác đều:
\(S=6,5^2=42,25\left(cm^2\right)\)
Thể tích của hình chóp tứ giác đều là:
\(V=\dfrac{1}{3}\cdot S\cdot h=\dfrac{1}{3}\cdot42,25\cdot12=169\left(cm^3\right)\)