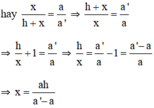Để đo chiều rộng AB của một khúc sông người ta dựng được ba điểm C, D, E thẳng hàng; ba điểm C, B, A thẳng hàng và BD song song với AE . Biết rằng CB = 34 m, CD = 32m, CE = 100 m. Tìm chiều rộng AB của khúc sông đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 6 2023
Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)
KV
31 tháng 12 2023
Ta có:
tan C = AB/AC
AB = AC.tan C
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng khúc sông là 71,51 m
KV
31 tháng 12 2023
Ta có:
tan C = AB/AC
AB = AC.tan C
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng khúc sông là 71,51 m
KV
1 tháng 1
Ta có:
tan ACB = AB/AC
⇒ AB = AC.tan ACB
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng của khúc sông là 71,51 m
14 tháng 5 2021
Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m
11 tháng 6 2021
Ta có :
\(\dfrac{NM}{AB}\) và \(\dfrac{CN}{CA}\) .
Vì \(\dfrac{NM}{AB}\) = \(\dfrac{CN}{CA}\) \(\Leftrightarrow\) AB = 1,5 . \(\dfrac{20}{1,25}\) = 24 ( m ) .
Vậy chiều cao AB của tòa nhà đó là 24 m .
CM
5 tháng 2 2018
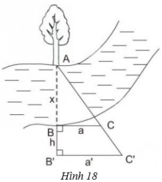
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 
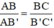(hệ quả định lý Talet)
