Tìm tỉ số của hai số
a) ; b = 70cm
b) a = 0,2m; b = 200cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

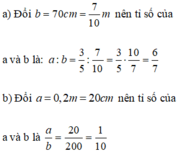

a, Tỉ số phần trăm của 28,5 và 50 là:
28,5 : 50. 100%= 57%
b, Tỉ số phần trăm của 2 1/2 và 3 1/3 là:
2 1/2 : 3 1/3 . 100% = 75%
Đ/s: a, 57%
b, 75%
- Chúc bạn học tốt!-

Tỉ số % của 2 số đó là:
a)8:60=0,1333...=13,33%
b)6,25:25=0,25=25%
c)1,6:8=0,2=20%

Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2

Ta có: a = 3/5m = 0,6m = 60cm
Tỉ số giữa 60cm và 70cm là 60 : 70 = 60/70 = 6/7

a, Thay m=14 vào pt* có
\(x^2-20x+14+5=0\)
⇔\(x^2-20x+19=0\)
⇔(x-1)(x-19)=0
⇔\(\left[{}\begin{matrix}x-1=0\\x-19=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=1\\x=19\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=1\\x=19\end{matrix}\right.\)khi và chỉ khi m=14

a: Để hàm số đồng biến thì m-2>0
=>m>2
b: Để hàm số nghịch biến thì m-2<0
=>m<2

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

a)
MSC: 18
Có:
\(\dfrac{5}{6}=\dfrac{5\times3}{6\times3}=\dfrac{15}{18}\)
b)
MSC: 24
Có:
\(\dfrac{3}{8}=\dfrac{3\times3}{8\times3}=\dfrac{9}{24}\)
\(\dfrac{7}{12}=\dfrac{7\times2}{12\times2}=\dfrac{14}{24}\)
a: \(\dfrac{5}{6}=\dfrac{5\cdot3}{6\cdot3}=\dfrac{15}{18}\)
17/18=17/18
b: \(\dfrac{3}{8}=\dfrac{3\cdot3}{8\cdot3}=\dfrac{9}{24}\)
\(\dfrac{7}{12}=\dfrac{7\cdot2}{12\cdot2}=\dfrac{14}{24}\)

a) Khi \(m=1\) ta có phương trình \(x^2-3x+1=0\)
\(\Delta=3^2-4=5\)
Phương trình có 2 nghiệm phân biệt \(x_1=\dfrac{3-\sqrt{5}}{2};x_2=\dfrac{3+\sqrt{5}}{2}\)
b) Xét phương trình \(x^2-3x+m=0\left(1\right)\)
\(\Delta=9-4m\)
PT có hai nghiệm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow9-4m>0\Leftrightarrow m< \dfrac{9}{4}\)
Áp dụng hệ thức Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m\end{matrix}\right.\)
Để \(x_1^2+x_2^2=2021\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=2021\)
\(\Leftrightarrow3^2-2m=2021\Leftrightarrow2m=-2012\Leftrightarrow m=-1006\) (TM)