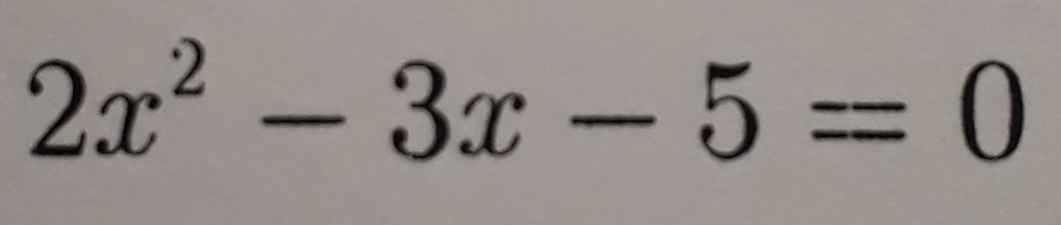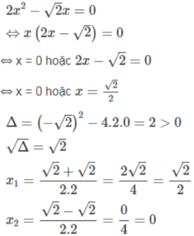Giải các phương trình sau bằng hai cách (phương trình tích; bằng công thức nghiệm) và so sánh kết quả tìm được: 3 5 x 2 + 6x = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
8 tháng 5 2018
Đúng(0)
Những câu hỏi liên quan
LV
2
23 tháng 9 2023
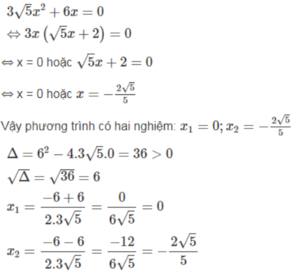
\(2x^2-3x-5=0 \\ \Leftrightarrow2x^2+2x-5x-5=0\\ \Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{5}{2};-1\right\}\)
T
23 tháng 9 2023
\(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2+2x-5x-5=0\)
\(\Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\)
Vậy \(x=\dfrac{5}{2};x=-1\) là các nghiệm của phương trình.
#\(Toru\)
PT
1
CM
24 tháng 4 2017
– x 2 + 5x – 6 = 0 ⇔ - x 2 + 2x + 3x – 6 = 0
⇔ - x(x – 2) + 3(x – 2) = 0 ⇔ (x – 2)(3 – x) = 0
⇔ x – 2 = 0 hoặc 3 – x = 0
x – 2 = 0 ⇔ x = 2
3 – x = 0 ⇔ x = 3
Vậy phương trình có nghiệm x = 2 hoặc x = 3.
PT
1
CM
24 tháng 12 2017
x 2 – 3x + 2 = 0 ⇔ x 2 – x – 2x + 2 = 0
⇔ x(x – 1) – 2(x – 1) = 0 ⇔ (x – 2)(x – 1) = 0
⇔ x – 2 = 0 hoặc x – 1 = 0
x – 2 = 0 ⇔ x = 2
x – 1 = 0 ⇔ x = 1
Vậy phương trình có nghiệm x= 2 hoặc x = 1
PT
1
CM
26 tháng 3 2017
2 x 2 + 5x + 3 = 0 ⇔ 2 x 2 + 2x + 3x + 3 = 0
⇔ 2x(x + 1) + 3(x + 1) = 0 ⇔ (2x + 3)(x + 1) = 0
⇔ 2x + 3 = 0 hoặc x + 1 = 0
2x + 3 = 0 ⇔ x = -1,5
x + 1 = 0 ⇔ x = -1
Vậy phương trình có nghiệm x = -1,5 hoặc x = -1
PT
1
CM
13 tháng 6 2018
4 x 2 – 12x + 5 = 0 ⇔ 4 x 2 – 2x – 10x + 5 = 0
⇔ 2x(2x – 1) – 5(2x – 1) = 0 ⇔ (2x – 1)(2x – 5) = 0
⇔ 2x – 1 = 0 hoặc 2x – 5 = 0
2x – 1 = 0 ⇔ x = 0,5
2x – 5 = 0 ⇔ x = 2,5
Vậy phương trình có nghiệm x = 0,5 hoặc x = 2,5
PT
1
CM
13 tháng 2 2018
Ta có: x 2 + x + 1 2 = 4 x - 1 2
⇔ [( x 2 +x +1) + (4x -1 )] [( x 2 +x +1) - (4x -1 )]=0
⇔ ( x 2 +5x)( x 2 -3x +2) =0 ⇔ x(x+5) ( x 2 -3x +2) =0
⇔ x =0 hoặc x+5 =0 hoặc x2 -3x +2 =0
x+5 =0 ⇔ x=-5
x 2 -3x +2 =0
∆ = - 3 2 -4.2.1 = 9 -8 =1 > 0
∆ = 1 =1
Vậy phương trình đã cho có 4 nghiệm:
x 1 =0 ; x 2 =-5 ; x 3 =2 ; x 4 =1