Nhờ mọi người giải giúp em với ạ
Lập bảng biến thiên và vẽ đò thị hàm số:
a) y = x - 3x - 2 ;
b) y = -2x^2 + 3x + 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)


a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3

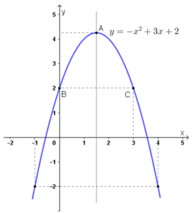
y = –x2 + 3x + 2 có a = –1 < 0, b = 3, c = 2:
+ Tập xác định D = R
+ Đồng biến trên 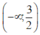 , nghịch biến trên
, nghịch biến trên 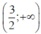
Bảng biến thiên:
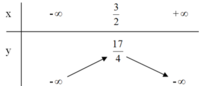
+ Đồ thị là parabol có:
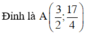
Trục đối xứng là đường thẳng x = 3/2
Giao điểm với trục tung là B(0 ; 2). Điểm đối xứng với B qua đường thẳng x = 3/2 là C(3 ; 2).
Đi qua các điểm (–1 ; –2) và (4 ; –2)

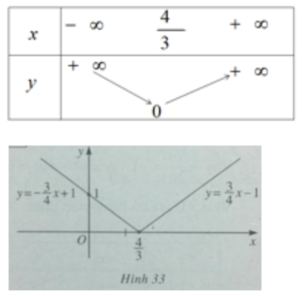
Bảng biến thiên và đồ thị của hàm số y = |-3x / 4 + 1| (h.33)

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=-\dfrac{\left(-3\right)^2-4\cdot1\cdot\left(-2\right)}{4}=-\dfrac{9+8}{4}=-\dfrac{17}{4}\end{matrix}\right.\)
=>Hàm số đồng biến khi x>3/2 và nghịch biến khi x<3/2
b: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-3}{2\cdot\left(-2\right)}=\dfrac{3}{4}\\y=-\dfrac{3^2-4\cdot\left(-2\right)\cdot5}{4}=-\dfrac{9+40}{4}=-\dfrac{49}{4}\end{matrix}\right.\)
=>Hàm số nghịch biến khi x>3/4; đồng biến khi x<3/4