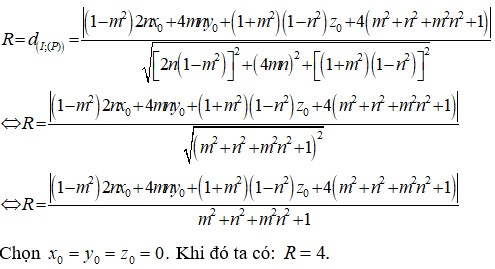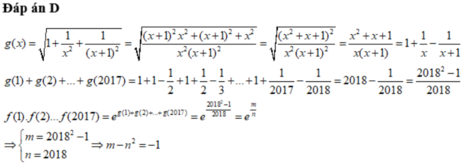cho m2+n2=1 ; a2+b2=1. c/m: -1 \(\le\) am + bn \(\le\) 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
4 tháng 10 2023
Nếu m hoặc n chia hết cho 3 thì hiển nhiên \(nm\left(m^2-n^2\right)⋮3\)
Nếu cả m và n đều không chia hết cho 3 thì \(m^2,n^2\) đều chia 3 dư 1 (tính chất của số chính phương). Do đó \(m^2-n^2⋮3\) nên \(mn\left(m^2-n^2\right)⋮3\)
Vậy \(mn\left(m^2-n^2\right)⋮3\) với mọi cặp số nguyên m, n.
BN
26 tháng 9 2021
Ta có M 2 ^ − N 0 ^ = 35 ° (đề bài) (1)
Lại có a // b nên M 2 ^ + N 2 ^ = 180 ° (2) (hai góc trong cùng phía)
Từ (1) và (2) ⇒ 2 M 2 ^ = 215 ° ⇒ M 2 ^ = 107.5 ° .
Từ (1) có N 1 ^ = 107.5 ° − 35 ° = 72.5 ° .
Do a // b nên : N 2 ^ = M 2 ^ = 107.5 ° (hai góc so le trong).
N 1 ^ = M 2 ^ = 72.5 ° (hai góc so le trong)
PD
0
CM
9 tháng 7 2019
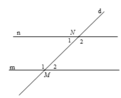
Ta có M 1 ^ − N 1 ^ = 50 ° (đề bài) (1)
Lại có n // m nên M 1 ^ + N 1 ^ = 180 ° (2) (hai góc trong cùng phía)
Từ (1) và (2) ⇒ 2 M 1 ^ = 230 ° ⇒ M 1 ^ = 115 ° .
Từ (1) có N 1 ^ = 115 ° − 50 ° = 65 ° .
Do n // m nên : N 2 ^ = M 1 ^ = 115 ° (hai góc so le trong).
N 1 ^ = M 2 ^ = 65 ° (hai góc so le trong)