Đề cho a , b ,c ,d thỏa mãn a + b = c + d ; a^2 + b^2 = c^2 + d^2 CMR : a^2002 + b^2002 = c^2002 + d^2002
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
Theo đầu bài ta có: AC2 + BD2 = AD2 + BC2 nên AC2 - AD2 = BC2 - BD2
Suy ra:
![]()
Hay
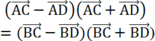
Tương đương
![]()
![]()
![]()

Câu trắc nghiệm này kinh thật :D
\(P=\left(1+36abc\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+36\left(ab+bc+ca\right)\)
\(P=\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)+36\left(ab+bc+ca\right)\)
\(P=\dfrac{a^2+b^2}{ab}+\dfrac{b^2+c^2}{bc}+\dfrac{c^2+a^2}{ca}+3+36\left(ab+bc+ca\right)\)
\(P=\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{\left(2a+2b+2c\right)^2}{ab+bc+ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{4}{ab+bc+ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge2\sqrt{\dfrac{144\left(ab+bc+ca\right)}{ab+bc+ca}}-3=21\)
Vậy \(P\ge21\)

a/b = b/c = c/d = (a+b+c)/(b+c+d)
=> (a+b+c/b+c+d)^6054 = (a/b)^6054

Ta có: a2 + b2 = c2 + d2
=>a2-c2=d2-b2
=>(a-c)(a+c)=(d-b)(d+b) (1)
Lại có: a + b = c + d
=>a-c=d-b
Nếu a=c => b=d hiễn nhiên biểu thức:
a2002 + b2002 = c2002 + d2002 đúng. (II)
Nếu a c =>b
c =>b d
d
=>a-c=d-b 0
0
Khi đó biểu thức (1) trở thành:
a+c=b+d (a-c, d-b khác không nên ta có thể đơn giản)
mà: a + b = c + d
cộng hai biểu thức theo vế ta được:
2a+b+c=b+c+2d
=>2a=2d
=>a=d
=>b=c
Vì a=d và b=c nên biểu thức a2002 + b2002 = c2002 + d2002 đúng. (I)
Kết luận: với điều kiện đềcho ta luôn có: a2002 + b2002 = c2002 + d2002.
Ta có: a2 + b2 = c2 + d2
=>a2-c2=d2-b2
=>(a-c)(a+c)=(d-b)(d+b) (1)
Lại có: a + b = c + d
=>a-c=d-b
Nếu a=c => b=d hiễn nhiên biểu thức:
a2002 + b2002 = c2002 + d2002 đúng. (II)
Nếu a c =>b
c =>b d
d
=>a-c=d-b 0
0
Khi đó biểu thức (1) trở thành:
a+c=b+d (a-c, d-b khác không nên ta có thể đơn giản)
mà: a + b = c + d
cộng hai biểu thức theo vế ta được:
2a+b+c=b+c+2d
=>2a=2d
=>a=d
=>b=c
Vì a=d và b=c nên biểu thức a2002 + b2002 = c2002 + d2002 đúng. (I)
Suy ra với điều kiện đềcho ta luôn có: a2002 + b2002 = c2002 + d2002.