Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
Tam giác ABC cân tại A
=> BAH=CAH
Ta lại có:
AI=AK
Gọi giao điểm của AH và IK là M
Xét ΔAIMΔAIM và ΔAKMΔAKM có:
AT=AK ( gt )
BAH=CAH(cmt)
AM chung
=> ΔAIMΔAIM= ΔAKMΔAKM (c.g.c)
=> IM=KM
=> I là đối xứng của K qua AH
(đ.p.c.m)
:))

1) Xét ΔCAB vuông tại A và ΔEAD vuông tại A có
AB=AD(gt)
AC=AE(gt)
Do đó: ΔCAB=ΔEAD(hai cạnh góc vuông)
Suy ra: BC=DE(hai cạnh tương ứng)
2) Xét ΔABD có AB=AD(gt)
nên ΔABD cân tại A(Định nghĩa tam giác cân)
Xét ΔABD cân tại A có \(\widehat{BAD}=90^0\)(gt)
nên ΔABD vuông cân tại A(Định nghĩa tam giác vuông cân)

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
=>BC=DE
b: Xét ΔABD vuông tại A có AB=AD
nên ΔABD vuông cân tại A
=>\(\widehat{ABD}=\widehat{ADB}=45^0\)
Xét ΔAEC vuông tại A có AE=AC
nên ΔAEC vuông cân tại A
=>\(\widehat{AEC}=\widehat{ACE}=45^0\)
Ta có: \(\widehat{ABD}=\widehat{AEC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//CE

Vì tam giac ABC cân ở A nên góc B=góc C=(180 độ- góc A)/2
Vì tam giac ADE cân ở A nên góc D=góc E=(180 độ- góc A)/2
=>Góc B=Góc D=>DE//BC
Vì tam giác ABC cân ở A nên trung tuyến AI cũng là đường cao
=>AI vuông góc với BC mà BC//DE
=>AI vuông góc với DE
Vì tam giác ABC cân ở A nên góc B = góc C = ( 180 độ - góc A ) / 2
Vì tam giác ADE cân ở A nên góc D = góc E = ( 180 độ - góc A ) / 2
=> góc B = góc D => DE/BC.
Vì tam giác ABC cân ở A nên tung tuyến AI cũng là đường cao.
=> AI vuông góc với BC mà BC//DE
=> AI vuông góc với DE

A B C I K H O
Gọi giao điểm của IK và AH là O.
Vì ΔABC cân tại A và AH là đường cao
=> AH đồng thời cũng là tia phân giác của ΔABC
hay AO là tia phân giác của \(\widehat{IAK}\)
=> \(\widehat{IAO}=\widehat{OAK}\)
Xét ΔAIO và ΔAKO có: \(\left\{{}\begin{matrix}AI=AK\left(gt\right)\\\widehat{IAO}=\widehat{KAO}\\AO
chung\end{matrix}\right.\)
=> ΔAIO = ΔAKO(c.g.c)
=>IO=KO(2 cạnh tương ứng)
Xét ΔAIK cân tại A (AI=AK) có AO là đường trung tuyến
=> AO là đương trung trực của \(\Delta\) AIK
=> I đối xứng với K qua AH
=>đpcm
Ta có: AI+IB=AB(I nằm giữa A và B)
AK+KC=AC(K nằm giữa A và C)
mà AI=AK(gt)
và AB=AC(ΔABC cân tại A)
nên IB=KC
Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(Hai cạnh tương ứng)
Xét ΔIBH và ΔKCH có
IB=KC(cmt)
\(\widehat{B}=\widehat{C}\)(ΔBAC cân tại A)
BH=CH(cmt)
Do đó: ΔIBH=ΔKCH(c-g-c)
Suy ra: HI=HK(Hai cạnh tương ứng)
Ta có: AI=AK(gt)
nên A nằm trên đường trung trực của IK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: HI=HK(cmt)
nên H nằm trên đường trung trực của IK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AH là đường trung trực của IK
hay I đối xứng với K qua AH(đpcm)

A B C H D E
a) *Chứng minh HD = HE.
Tam giác ABC cân tại A có đường cao AH xuất phát từ đỉnh A nên đồng thời là đường phân giác.
\(\Rightarrow\)^HAB = ^HAC mà D \(\in\)AB, E \(\in\)AC nên ^HAD = ^HAE . Từ đây dễ c/m \(\Delta\)HEA = \(\Delta\) HDA (c.g.c)\(\Rightarrow\) HD = HE (hai cạnh tương ứng)
*Chứng minh IA = IH: Có gì sai không bạn? Vẽ hình ra thấy rõ ràng nó không bằng nhau rồi mà? (đó chính là lí do mình ko để điểm I trong hình bên trên). Nếu đề vẫn đúng thì mình chịu nha!

A B C H I K
a) Ta có AI = AK ; AB = AC => AI / AB = AK/ AC => IK // BC (Định lí Ta lét)
Tam giác ABC cân tại A có AH là đường cao => AH I BC
=> AH I IK
Mặt khác, tam giác AIK cân tại A : AH là đường cao nên đồng thời là đường trung trực
=> I và K đối xứng qua AH

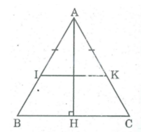
Ta có: △ ABC cân tại A; AH ⊥ BC (gt)
Suy ra: AH là tia phân giác của góc A
Lại có: AI = AK (gt)
Suy ra: ∆ AIK cân tại A
Do AH là tia phân giác của góc A
Nên AH là đường trung trực của IK
Vậy I đối xứng với K qua AH.
Ta có :
Tam giác ABC cân tại A
=> BAH=CAH
Ta lại có:
AI=AK
Gọi giao điểm của AH và IK là M
Xét ΔAIMΔAIM và ΔAKMΔAKM có:
AT=AK ( gt )
BAH=CAH(cmt)
AM chung
=> ΔAIMΔAIM= ΔAKMΔAKM (c.g.c)
=> IM=KM
=> I là đối xứng của K qua AH
(đ.p.c.m)
:))
Ta có :
Tam giác ABC cân tại A
=> BAH=CAH
Ta lại có:
AI=AK
Gọi giao điểm của AH và IK là M
Xét ΔAIMΔAIM và ΔAKMΔAKM có:
AT=AK ( gt )
BAH=CAH(cmt)
AM chung
=> ΔAIMΔAIM= ΔAKMΔAKM (c.g.c)
=> IM=KM
=> I là đối xứng của K qua AH
(đ.p.c.m)