Cho hình chóp S.ABC có đáy vuông cân ở B, ; ; . Gọi G là trọng tâm của , mp đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S. Tính V.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

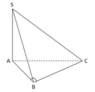
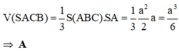
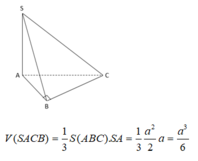
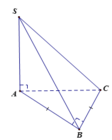
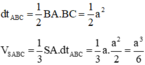

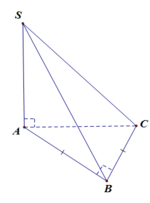
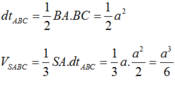

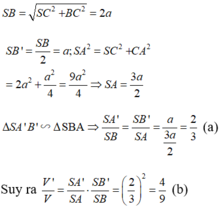
Trong (SBC) qua G kẻ M N / / B C M ∈ S B ; N ∈ S C . Khi đó mặt phẳng đi qua AG và song song với BC chính là mặt phẳng (AMN). Mặt phẳng này chia khối chóp thành 2 khối S.AMN và AMNBC.
Gọi H là trung điểm của BC.
Vì M N / / B C
Theo định lí Ta-lét ta có:
Mà
Vậy
Chọn A.