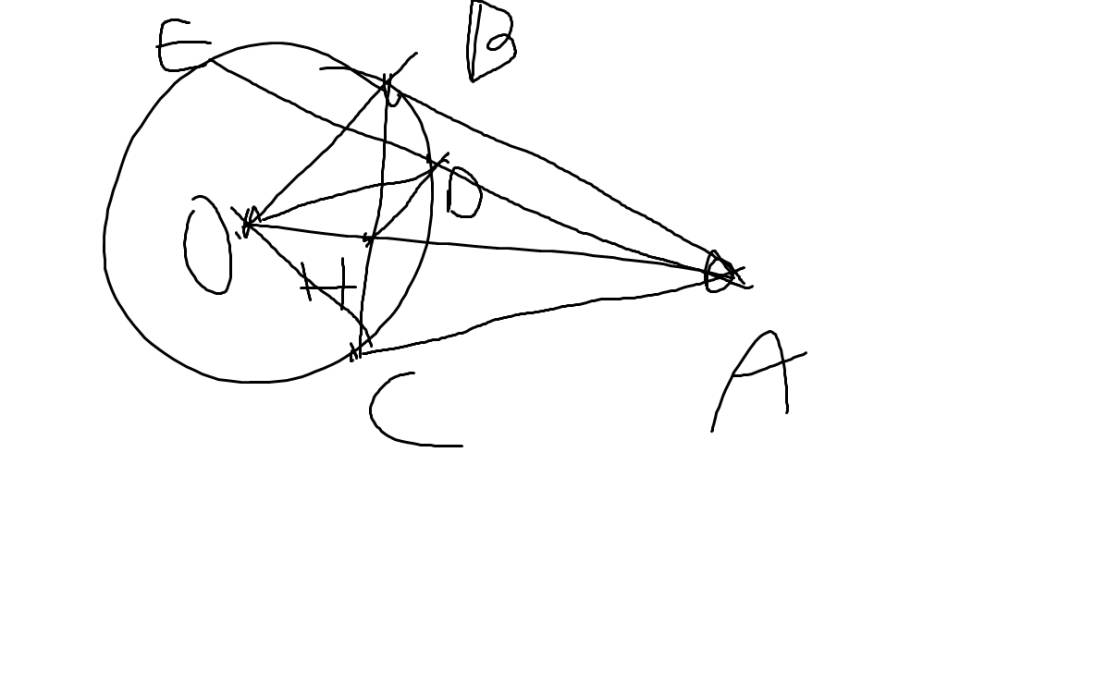
Từ điểm A ở ngoài (O; R) vẽ hai tiếp tuyến AB, AC( B, C là hai tiếp điểm). Gọi H là giao điểm của OA và BC a) Chứng minh OA vuông góc BC và OH.OA = R2 b) Vẽ đường kính BE của (O), AE cắt (O) tại D. Chứng minh ED.EA = 4OH.OA c) Vẽ CI vuông góc BE tại I, AE cắt CI tại K. Chứng minh HK // BE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 5 2020
Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^
30 tháng 11 2023
c: Xét (O) có
M,O,N thẳng hàng
=>MN là đường kính của (O)
OA là đường trung trực của BC(cmt)
=>OA\(\perp\)BC tại H và H là trung điểm của BC
\(\widehat{HCM}+\widehat{HMC}=90^0\)(ΔHMC vuông tại H)
\(\widehat{ACM}+\widehat{OCM}=\widehat{OCA}=90^0\)
mà \(\widehat{OCM}=\widehat{HMC}\)(ΔOMC cân tại O)
nên \(\widehat{HCM}=\widehat{ACM}\)
=>CM là phân giác của góc ACB(5)
Xét (O) có
ΔNCM nội tiếp
NM là đường kính
Do đó: ΔNCM vuông tại C
=>CM\(\perp\)CN(6)
Từ (5),(6) suy ra CN là phân giác góc ngoài tại đỉnh C của ΔACH
Xét ΔACH có CN là phân giác góc ngoài tại đỉnh C
nên \(\dfrac{CA}{CH}=\dfrac{NA}{NH}\left(7\right)\)
Xét ΔACH có CM là phân giác góc trong tại đỉnh C
nên \(\dfrac{CA}{CH}=\dfrac{MA}{MH}\left(8\right)\)
Từ (7) và (8) suy ra \(\dfrac{NA}{NH}=\dfrac{MA}{MH}\)
=>\(NA\cdot MH=NH\cdot MA\)
30 tháng 11 2023
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>ΔABC cân tại A
b: AB=AC
=>A nằm trên đường trung trực của BC(1)
OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại trung điểm của BC
=>AO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=OB\cdot OB=OB\cdot OC\)
PT
1
30 tháng 11 2023
c: Xét (O) có
M,O,N thẳng hàng
=>MN là đường kính của (O)
OA là đường trung trực của BC(cmt)
=>OA\(\perp\)BC tại H và H là trung điểm của BC
\(\widehat{HCM}+\widehat{HMC}=90^0\)(ΔHMC vuông tại H)
\(\widehat{ACM}+\widehat{OCM}=\widehat{OCA}=90^0\)
mà \(\widehat{OCM}=\widehat{HMC}\)(ΔOMC cân tại O)
nên \(\widehat{HCM}=\widehat{ACM}\)
=>CM là phân giác của góc ACB(5)
Xét (O) có
ΔNCM nội tiếp
NM là đường kính
Do đó: ΔNCM vuông tại C
=>CM\(\perp\)CN(6)
Từ (5),(6) suy ra CN là phân giác góc ngoài tại đỉnh C của ΔACH
Xét ΔACH có CN là phân giác góc ngoài tại đỉnh C
nên \(\dfrac{CA}{CH}=\dfrac{NA}{NH}\left(7\right)\)
Xét ΔACH có CM là phân giác góc trong tại đỉnh C
nên \(\dfrac{CA}{CH}=\dfrac{MA}{MH}\left(8\right)\)
Từ (7) và (8) suy ra \(\dfrac{NA}{NH}=\dfrac{MA}{MH}\)
=>\(NA\cdot MH=NH\cdot MA\)
8 tháng 12 2023
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD
