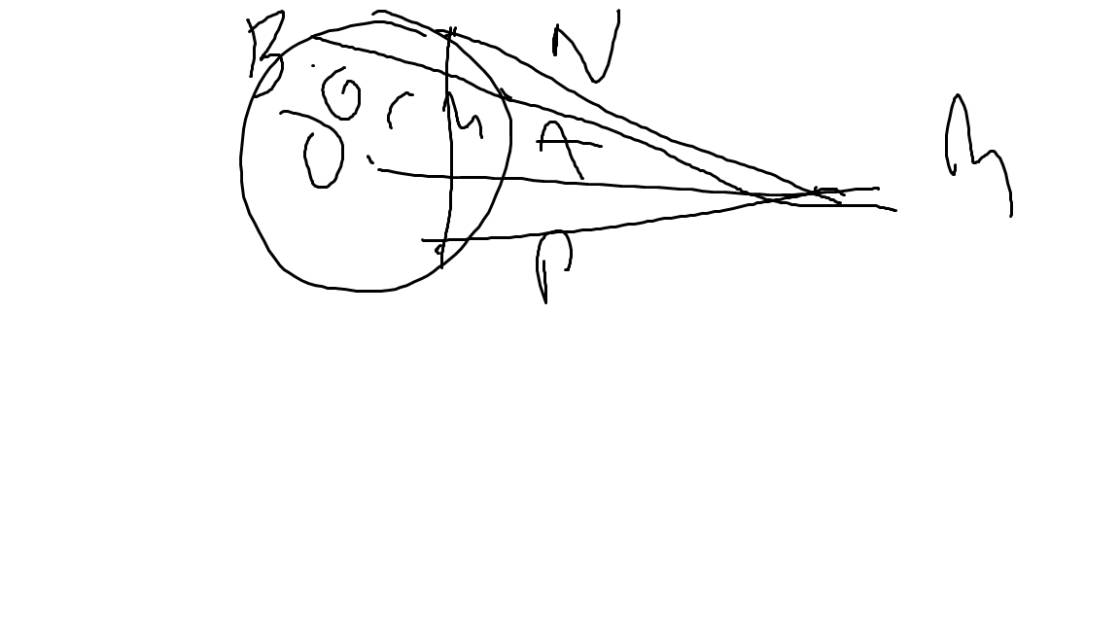
Từ một điểm M ở bên ngoài đường tròn (O ; 6cm) kẻ hai tiếp tuyến MN; MP với đường tròn (N; P € (O)) cắt tuyến MAB của O sao cho AB = 6 cm a, chứng minh OPMN là tứ giác nội tiếp b, tính độ dài đoạn thẳng MN biết MO = 10 CM C, gọi h là trung điểm đoạn thẳng AB. So sánh góc MO^N với góc và MH^N d, diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của đường tròn tâm O đã cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi bán kính của đường tròn (O) là R
Ta có:MB=MA+AB = MA + 2R
Suy ra: MA =MB – 2R
Ta lại có: M T 2 = MA.MB (cmt)
Suy ra: M T 2 = (MB- 2R).MB = M B 2 – 2R.MB
![]()

M A B C 1
xét tam giác MCA và tam giác MAB có C1 = MAB ( 2 góc cùng chắn cung AB )
góc M chung
=> tam giác MCA đồng dạng tam giác MAB (g-g )
=> MA2 = MB.MC

a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔAKM và ΔAMI có
góc AMK=góc AIM
góc MAK chung
=>ΔAKM đồng dạng với ΔAMI
=>AK/AM=AM/AI
=>AM^2=AI*AK
Xét ΔABM và ΔAMC có
góc AMB=góc ACM
góc BAM chung
=>ΔABM đồng dạng với ΔAMC
=>AB/AM=AM/AC
=>AM^2=AB*AC=AK*AI

a: góc ACN=1/2*sđ cung MC
góc BAD=góc MDC=1/2*sđ cung MC
=>góc ACN=góc BAD
b: Xét ΔNAM và ΔNCA có
góc NAM=góc NCA
góc N chung
=>ΔNAM đồng dạng với ΔNCA
=>NA/NC=NM/NA
=>NA^2=NM*NC

2: Xét tứ giác MBOC có
\(\widehat{MBO}+\widehat{MCO}=180^0\)
Do đó: MBOC là tứ giác nội tiếp

a) Xét \(\Delta BMT\) và \(\Delta TMA\) có:
\(\widehat{M}\) chung
\(\widehat{B}=\widehat{MTA}\) (cùng chắn \(\stackrel\frown{AT}\))
\(\Rightarrow\Delta BMT\sim\Delta TMA\)
\(\Rightarrow\dfrac{MT}{MA}=\dfrac{MB}{MT}\Rightarrow MT^2=MA.MB\left(\text{Đ}PCM\right)\)


hỏi chấm