Chứng tỏ ; Nếu a/b=b/c thì a^2+b^2 / b^2+c^2 = a/c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
MN ơi giải giúp em bài này với : a) chứng tỏ tia A3=B1 b) chứng tỏ A3 + B4= 180 độ c) chứng tỏ A1=B1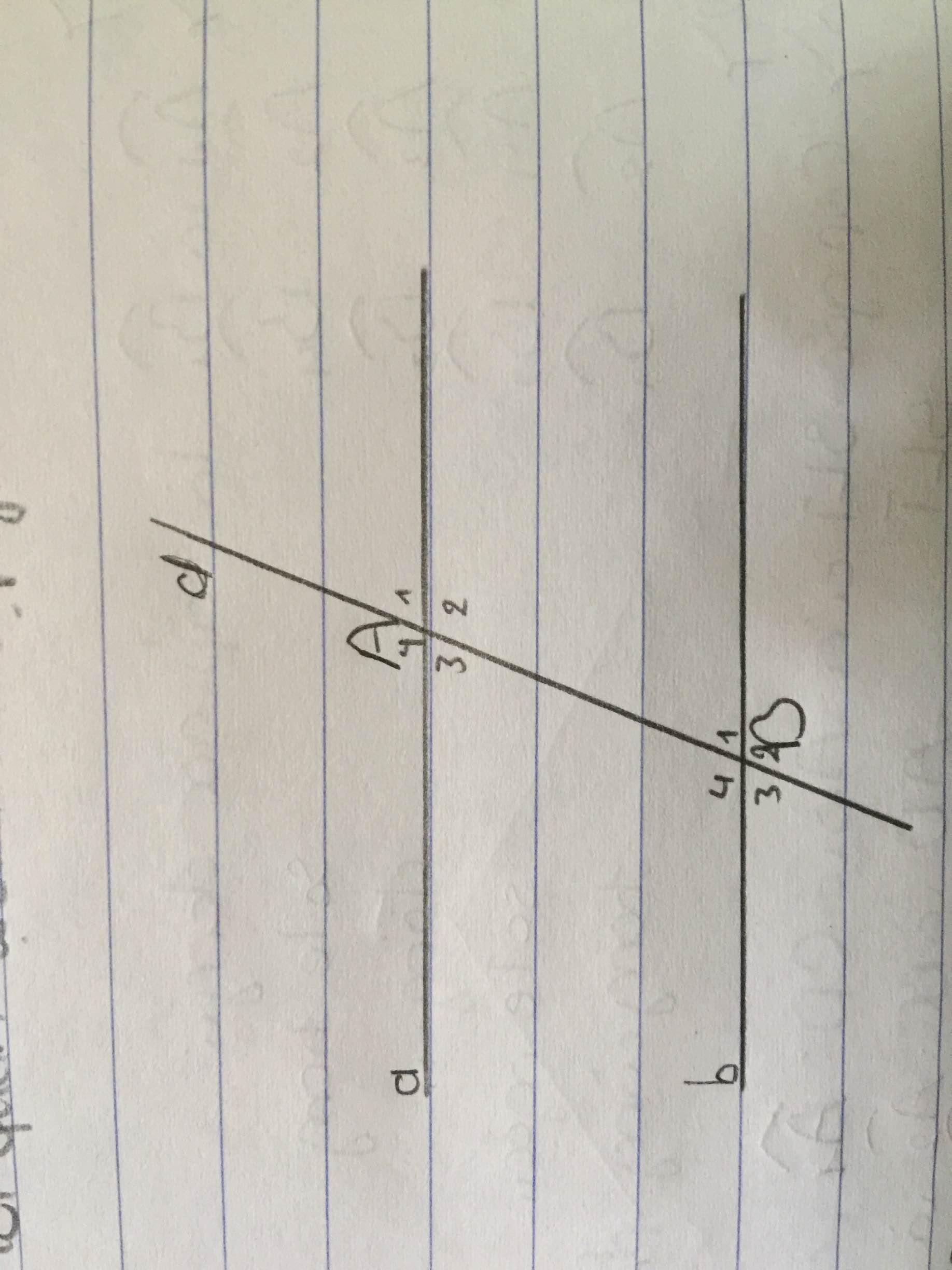
4
KV
22 tháng 10 2023
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
22 tháng 7 2023
a: A=3(1+3+3^2+3^3)+...+3^129(1+3+3^2+3^3)
=40(3+...+3^129) chia hết cho 40
b: A=(3+3^2+3^3)+....+3^129(3+3^2+3^3)
=39(1+...+3^129) chia hết cho 39
c: A chia hết cho 40
A chia hết cho 3
=>A chia hết cho BCNN(40;3)=120
CM
14 tháng 7 2017
a) ΔADB và ΔABC vuông có ∠B chung ∠ ΔADB ∼ ΔCAB (g.g)
b) Vì ∠B = 2∠C (gt) ∠ ∠B1 = ∠B2 = ∠C
Do đó hai tam giác vuông ABE và ACB đồng dạng (g.g)
c) Ta có ΔADB ∼ ΔCAB (cmt)
Theo tính chất đường phân giác ta có :
d) Ta có AB = 2BD (gt)
J
4 tháng 1 2022
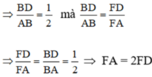
+ Buôn bán tấp nập, chợ búa mọc lên ở nhiều nơi.
+ Xuất hiện một số thương nhân, thường tập trung ở các đô thị, thương cảng.
+ có nhiều phường thủ công, nhiều chợ lớn thu hút người buôn bán các nơi.
+
3 tháng 10 2019
a, b : 7 dư 4 ; c chia 7 dư 3 mà 4 + 3 = 7 chia hết cho 7
=> b+c chia hết cho 7
b, ( tương tự dựa vào đó mà lm nhé mày ) biết chưa quỷ cái
Ta có : \(\dfrac{a}{b}=\dfrac{b}{c}\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{b^2}{c^2}=\dfrac{ab}{bc}\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{b^2}{c^2}=\dfrac{a}{c}\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\dfrac{a^2}{b^2}=\dfrac{b^2}{c^2}=\dfrac{a}{c}=\dfrac{a^2+b^2}{b^2+c^2}\)
\(\Rightarrow\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a}{c}\left(đpcm\right)\)