Cho tam giác ABC biết góc A=90o, AB=AC; MB=MC=1/2 BC
E thuộc đoạn CM. Kẻ BK,CH vuông góc với AE
CMR MBK là tam giác vuông cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) + Δ ABC vuông tại A, có 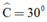
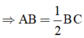
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của 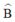
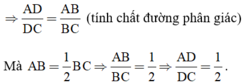
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
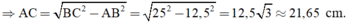
+ Chu vi tam giác ABC là:
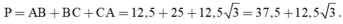
+ Diện tích tam giác ABC là:
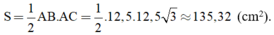

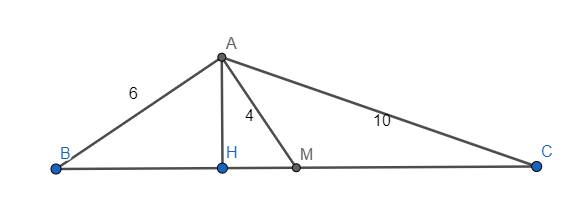
Hạ \(AH\perp BC\) tại H. Đặt \(MB=MC=x;HM=y;AH=h\)
Theo định lý Pythagoras: \(\left\{{}\begin{matrix}AH^2+HM^2=AM^2\\AH^2+BH^2=AB^2\\AH^2+CH^2=AC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+\left(x-y\right)^2=36\\h^2+\left(x+y\right)^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+x^2+y^2-2xy=36\\h^2+x^2+y^2+2xy=100\end{matrix}\right.\)
Cộng theo vế của 2 pt thứ 2 và thứ 3 của hệ này, ta được:
\(2\left(h^2+x^2+y^2\right)=136\)
\(\Leftrightarrow x^2+\left(h^2+y^2\right)=68\)
\(\Leftrightarrow x^2+16=68\)
\(\Leftrightarrow x^2=52\) hay \(BM^2=52\)
Mà ta lại có \(AB^2+AM^2=6^2+4^2=52\)
\(\Rightarrow AB^2+AM^2=BM^2\) \(\Rightarrow\Delta ABM\) vuông tại A \(\Rightarrow\) đpcm
Gọi H là điểm đối xứng với A qua M
Xét tam giác AMB và tam giác HMC có:
\(\left\{{}\begin{matrix}HM=AM\\\widehat{AMB}=\widehat{HMC}\\MB=MC\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta HMC\left(c.g.c\right)\)
\(\Rightarrow HC=AB=6cm\)
Xét tam giác HAC có:
\(AH^2+HC^2=10^2\left(8^2+6^2=10^2\right)\)
\(\Rightarrow\widehat{AHC}=90^o\)
Mà \(\Delta AMB=\Delta HMC\)
\(\Rightarrow\widehat{MAB}=\widehat{MHC}=90^o\left(đpcm\right)\)

Xét △ABC và △AED có
AB=AE(gt)
BAC =EAD( đối đỉnh)
AC=AD(gt)
Vậy △ABC=△AED(c-g-c)

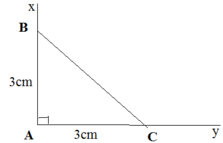
- Cách vẽ:
+ Vẽ góc xAy = 90o
+ Trên tia Ax vẽ đoạn thẳng AB = 3cm
+ Trên tia Ay vẽ đoạn thẳng AC = 3cm
+ Vẽ đoạn thẳng BC
Ta được tam giác ABC là tam giác cần vẽ
- Đo các góc B và C ta được góc B = góc C = 45º

Xét \(\Delta AMN\) có : \(AM+AN>MN\)
Xét \(\Delta ABC\) có : \(AB+AC>BC\)
Mà \(\left\{{}\begin{matrix}AM< AB\\AN< AC\end{matrix}\right.\) \(\Leftrightarrow AB+AC>AM+AN\)
\(\Leftrightarrow BC>MN\)