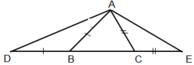
Cho tam giác ABC có AB=AC. Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm D và E sao cho BD= CE; M là trung điểm của BC.
a) CMR: AD= AE
b) CMR: AM là tia phân giác của góc DAE
c) Từ B và C kẻ BH và CK theo thứ tự vuông góc với AD và AE. CMR: BH= CK ( H€ AD, K€ AE )
d) CMR: AM, BH, CK đồng quy
( Mình chứng minh xong câu a,b,c mong các bạn giúp mình câu d). Cảm ơn!


a, tam giác ABC cân tại A (gt)
=> góc ABC = góc ACB (đl)
góc ABC + góc ABD = 180
góc ACB + góc ACE = 180
=> góc ABD = góc ACE
xét tam giác DBA và tam giác ECA có : BD = CE (gt)
AB = AC (gT)
=> tam giác DBA = tam giác ECA (c-g-c)
=> AD = AE (đn)
b, BM = CM do M là trđ của BC (gt)
BD = CE (gt)
BM + BD = DM
MC + CE = ME
=> MD = ME
xét tam giác AMD và tam giác AME có : AM chung
AD = AE (Câu a)
=> tam giác MAD = tam giác MAE (c-c-c)
=> góc DAM = góc EAM (đn) mà AM nằm giữa AD và AE
=> AM là pg của góc EAD (Đn)
c, tam giác DAM = tamg iacs EAM (câu b)
=> góc ADE = góc AED (đn)
xét tam giác DBH và tam giác ECK có : BD = CE (gt)
góc BHD = góc CKE = 90
=> tam giác DBH = tam giác ECK (ch-gn)
=> BH = CK (đn)