Cho tam giác ABC cân tại A; M, N lần lượt là trung điểm của AB, AC
a) Chứng minh tứ giác BCNM là hình thang cân
b) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh tam giác ADE là tam guacs cân
c) Gọi I là trung điểm của BC. Chứng minh AI là đường trung trực của đoạn thẳng BC và chứng minh ba đường thẳng AI, DN, EM đồng quy tại một điểm.
d) Chứng minh BD.BE + AB2 = AD2
Mấy bạn ai biết câu nào thì làm giúp mình với mình cảm ơn rất nhiều ạ

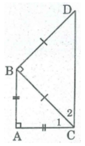
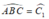
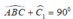 ( tính chất tam giác vuông).
( tính chất tam giác vuông).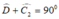
A B C M N E D I
a) Vì AM = MB và AN =NC
=> MN là đường trung bình cảu tam giác ABC
=> MN // BC
=> Tứ giác BCNM là hình thang
Vì tam giác ABC cân tại A
=> C = B
=> hình thang BCNM cân
b) ABD + ABE = 180 ( kề bù )
ACE + ACD = 180 ( kề bù )
mà ABE = ACD ( tam giác ABC cân tại A )
=> ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( tam giác ABC cân tại A )
ABD = ACE ( cm trên )
BD = CE ( GT )
=> tam giác ABD = tam giác ACE ( c.g.c )
=> AD = AE ( 2 cạnh tương ứng )
=> tam giác ADE cân tại A
Còn 2 phần cuối mk đang nghĩ
Cám ơn bạn đã giúp mình câu ab nha