cho tam giac ABC co hai duong cao BE,CF giao tai H. gọi I là trung điểm AH; K là trung điểm BC. biết AH=6 BC=8 tính IK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tư giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
Xét tứ giác CDHE có
góc CDH+góc CEH=180 độ
=>CDHE là tứ giác nội tiếp
b: CDHE là tứ giác nội tiếp
=>gó BED=góc FCB
góc FEH=góc BAD
mà góc FCB=góc BAD
nên góc BED=góc FEB
=>EB là phân giác của góc FED
c: góc IEO=góc IEH+góc OEH
=góc IHE+góc OBE
=góc BHD+góc CBH=90 độ
=>IE là tiếp tuyến của (O)

a: \(BC=\sqrt{9^2+6^2}=3\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{6\cdot9}{3\sqrt{13}}=\dfrac{18\sqrt{13}}{13}\left(cm\right)\)
b: Xét ΔEBF vuông tạiE và ΔEDC vuông tại E có
\(\widehat{EBF}=\widehat{EDC}\)
Do đó: ΔEBF\(\sim\)ΔEDC
d: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: BA=BE và DA=DE
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DO đó: ΔADF=ΔEDC
Suy ra: AF=EC
=>BF=BC
=>ΔBFC cân tại B
mà BD là đường phân giác
nên BD la đường cao

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc AHG=góc BHD=90 độ-góc HBD=góc ACB
góc AGH=1/2*sđ cung AB=góc ACB
=>góc AHG=góc AGH
=>ΔAGH cân tại A

 1.
1.
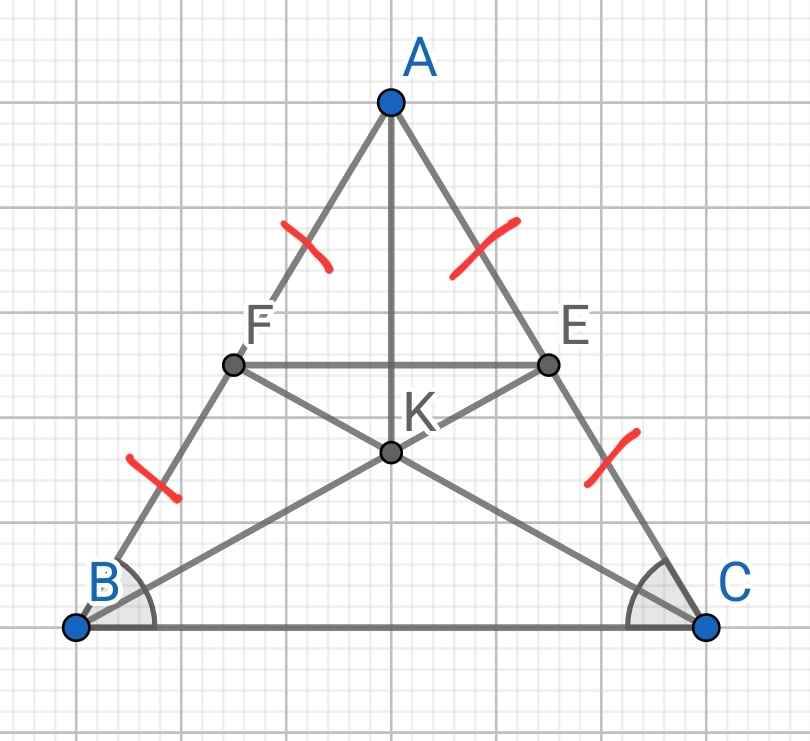
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB (1)
Do BE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AC
⇒ AE = CE = AC/2 (2)
Do CF là đường trung tuyến của ∆ABC (gt)
⇒ F là trung điểm của AB
⇒ AF = BF = AB/2 (3)
Từ (1), (2) và (3) ⇒ BF = CE
Do ∠ABC = ∠ACB (cmt)
⇒ ∠FBC = ∠ECB
Xét ∆BFC và ∆CEB có:
BF = CE (cmt)
∠FBC = ∠ECB (cmt)
BC chung
⇒ ∆BFC = ∆CEB (c-g-c)
⇒ CF = BE (hai cạnh tương ứng)
Hay BE = CF
b) Do ∆BFC = ∆CEB (cmt)
⇒ ∠BCF = ∠CBE (hai góc tương ứng)
⇒ ∠BCK = ∠CBK
∆BKC có:
∠BCK = ∠CBK (cmt)
⇒ ∆BKC cân tại K
c) Do ∆BKC cân tại K (cmt)
⇒ BK = CK
Do ∠ABC = ∠ACB (cmt)
⇒ ∠ABK = ∠ABC - ∠CBK = ∠ACB - ∠BCK = ∠ACK
⇒ ∠FBK = ∠ECK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
∠FBK = ∠CEK (cmt)
BF = CE (cmt)
⇒ ∆BFK = ∆CEK (c-g-c)
⇒ FK = EK (hai cạnh tương ứng)
d) Sửa đề: Chứng minh ∆BFK = ∆CEK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
BF = CE (cmt)
FK = EK (cmt)
⇒ ∆BFK = ∆CEK (c-c-c)
2.
a) Từ (1), (2) và (3) ⇒ AF = AE
∆AEF có:
AE = AF (cmt)
⇒ ∆AEF cân tại A
b) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (4)
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF = (180⁰ - ∠FAE) : 2
⇒ ∠AFE = ∠AEF = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠ABC = ∠AFE
Mà ∠ABC và ∠AFE là hai góc đồng vị
⇒ EF // BC
c) Xét ∆AFK và ∆AEK có:
AF = AE (cmt)
AK chung
FK = EK (cmt)
⇒ ∆AFK = ∆AEK (c-c-c)