Question

[Đại Nam]

Cho \(\Delta\)ABC cân tại A. (\(\widehat{A}\)<90o). Vẽ BH \(\perp\)AC; CK \(\perp\)AB (H \(\in\)AC; K \(\in\) AB)

a)Chứng minh: AH=AK

b)Gọi I là giao điểm của BH và Ck. Chứng minh \(\widehat{KAI}=\widehat{HAI}\)

c)Đường thẳng Ai cắt BC tại D. Chứng minh AI vuông góc với BC tại D

d) Chứng minh: HK\(//\) BC

e) Nếu cho \(\widehat{BAC}\)= 120o thì\(\Delta\)HIK trở thành tam giác gì. Vì sao?

Answer 1

[Rosegoldzinger]

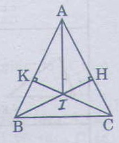
A B C I H K

a)

_ Xét \(\Delta\) AKC và \(\Delta\) AHI có :

+ góc AKC = gócÂHB = 90^o

⁺ A là góc chung

+ AB = AC ( gt )

=> \(\Delta\)AHB = \(\Delta\) AKC ( g.c.g)

=> AH = AK ( đpcm )

b)

_ Xét \(\Delta\) AKI và \(\Delta\) AHI có

+ góc AKI = góc AHI = 90⁰

+ AH = AK ( c/m trên )

+ AI là cạnh chung

=> \(\Delta\) AKI = \(\Delta\) AHI ( cạnh huyền - cạnh góc vuông )

=> góc KAI = gócHAI ( 2 góc tương ứng )

c)

_ Xét \(\Delta\) ABD và \(\Delta\) ACD có :

+ AB = AC ( gt )

+ AD chung

+ góc ADB = góc ACD = 90^o

=> \(\Delta\)ABD = \(\Delta\) ACD ( cạnh huyền - cạnh góc vuông )

=> AI \(\perp\) BC

Còn lại k biết lm