Cho \(\Delta ABC\) vuông tại A,đường cao AH. Kẻ HM\(\perp\)AB(M\(\in\)AB); HN\(\perp\)AC(N\(\in\)AC).Chứng minh rằng :
a) AM.AB=AN=AC
b)HB.HC=MA.MB+NA.NC
c)\((\frac{AB}{AC})^2\)=\(\frac{HB}{HC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
ΔABC vuông tại A
=>BC^2=AB^2+AC^2
=>\(BC^2=25+64=89\)
=>\(BC=\sqrt{89}\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}=\dfrac{8}{5}\)
=>\(\widehat{B}\simeq58^0\)
=>\(\widehat{C}=32^0\)
b: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
ΔAHB vuông tại H có HM vuông góc AB
nên AM*AB=AH^2; BM*BA=BH^2; AM*MB=HM^2
ΔAHC vuông tại H có HN làđường cao
nên AN*AC=AH^2;CN*CA=CH^2; NA*NC=NH^2
AM*MB+NA*NC
=HM^2+HN^2
=MN^2
c: AB^2/AC^2
\(=\dfrac{BH\cdot CB}{CH\cdot CB}=\dfrac{BH}{CH}\)

a) Để tính AC, ta sử dụng định lý Pythagoras trong tam giác vuông: AC^2 = AB^2 + BC^2. Với AB = 12cm và BC = 20cm, ta có: AC^2 = 12^2 + 20^2 = 144 + 400 = 544. Do đó, AC = √544 ≈ 23.32cm.
Để tính góc B, ta sử dụng công thức sin(B) = BC/AC. Với BC = 20cm và AC = 23.32cm, ta có: sin(B) = 20/23.32 ≈ 0.857. Từ đó, góc B ≈ arcsin(0.857) ≈ 58.62°.
Để tính AH, ta sử dụng công thức cos(B) = AH/AC. Với góc B ≈ 58.62° và AC = 23.32cm, ta có: cos(B) = AH/23.32. Từ đó, AH = 23.32 * cos(58.62°) ≈ 11.39cm.
b) Ta cần chứng minh AE.AC = AB^2 - HB^2. Vì ΔABC vuông tại A, ta có: AE = AB * sin(B) (theo định lý sin trong tam giác vuông) AC = AB * cos(B) (theo định lý cos trong tam giác vuông) HB = AB * sin(B) (theo định lý sin trong tam giác vuông)
Thay các giá trị vào biểu thức cần chứng minh: AE.AC = (AB * sin(B)) * (AB * cos(B)) = AB^2 * sin(B) * cos(B) = AB^2 * (sin(B) * cos(B)) = AB^2 * (sin^2(B) / sin(B)) = AB^2 * (1 - sin^2(B)) = AB^2 * (1 - (sin(B))^2) = AB^2 * (1 - (HB/AB)^2) = AB^2 - HB^2
Vậy, ta đã chứng minh AE.AC = AB^2 - HB^2.
c) Ta cần chứng minh AF = AE * tan(B). Vì ΔABC vuông tại A, ta có: AE = AB * sin(B) (theo định lý sin trong tam giác vuông) AF = AB * cos(B) (theo định lý cos trong tam giác vuông)
Thay các giá trị vào biểu thức cần chứng minh: AF = AB * cos(B) = AB * (cos(B) / sin(B)) * sin(B) = (AB * cos(B) / sin(B)) * sin(B) = AE * sin(B) = AE * tan(B)
Vậy, ta đã chứng minh AF = AE * tan(B).
d) Ta cần chứng minh tỉ lệ giữa các đường cao trong tam giác vuông ΔABC. CE/BF = AC/AB
Vì ΔABC vuông tại A, ta có: CE = AC * cos(B) (theo định lý cos trong tam giác vuông) BF = AB * cos(B) (theo định lý cos trong tam giác vuông)
Thay các giá trị vào biểu thức cần chứng minh: CE/BF = (AC * cos(B)) / (AB * cos(B)) = AC/AB
Vậy, ta đã chứng minh CE/BF = AC/AB.

a: Xét ΔAHC vuôg tại H và ΔAHB vuông tại H có
AB=AC
AH chung
DO đo: ΔAHC=ΔAHB
b: Xét tứ giác BMCN có
H là trung điểm của BC
H là trung điểm của MN
DO đó: BMCN là hình bình hành
Suy ra: BN//AC
c: Xét ΔAQH vuông tạiQ và ΔAMH vuông tại M có
AH chung
\(\widehat{QAH}=\widehat{MAH}\)
Do đó: ΔAQH=ΔAMH
Suy ra: HQ=HM
=>HQ=1/2MN
=>ΔMQN vuông tại Q
Xét ΔBQH vuông tạiQ và ΔBNH vuông tại N có
BH chung
HQ=HN
Do đó; ΔBQH=ΔBNH
Suy ra: BQ=BN
=>BH là đường trung trực của QN

a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
b: Xét tứ giác AHKC có
I là trung điểm chung của AK và HC
=>AHKC là hình bình hành
=>AC//KH
c: Ta có: AC//HK
AC//HM
HK,HM có điểm chung là H
Do đó: K,H,M thẳng hàng
Ta có: AMHN là hình chữ nhật
=>\(\widehat{NAH}=\widehat{NMH}\)
mà \(\widehat{NAH}=\widehat{CKH}\)(AHKC là hình bình hành)
nên \(\widehat{NMH}=\widehat{CKH}\)
Xét tứ giác MNCK có CN//MK
nên MNCK là hình thang
Hình thang MNCK có \(\widehat{CKM}=\widehat{NMK}\)
nên MNCK là hình thang cân
d: Ta có: AMHN là hình chữ nhật
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Xét ΔCAH có
CO,AI là các đường trung tuyến
CO cắt AI tại D
Do đó: D là trọng tâm của ΔCAH
=>\(AD=\dfrac{2}{3}AI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AK=\dfrac{1}{3}AK\)
=>AK=3AD

a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
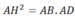


a) Ta có tứ giác MHNA là hình chữ nhật
\(\Rightarrow\widehat{AMN}=\widehat{AHN}\) ( góc nội tiếp cùng chắn cung AN)
mà \(\widehat{AHN}=\widehat{ACH}\) ( cùng phụ với \(\widehat{HAN}\) )
\(\Rightarrow\widehat{AMN}=\widehat{ACH}\)
Xét \(\Delta AMN\) và \(\Delta ACB\) có:
\(\left\{{}\begin{matrix}\widehat{AMN}=\widehat{ACH}\left(cmt\right)\\\widehat{MAN}chung\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(g.g\right)\)
\(\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\Rightarrow AM.AB=AN.AC\left(đpcm\right)\)
b) Xét \(\Delta AHB\) vuông tại H, \(MH\perp AB\) có:
\(MH^2=MA.MB\left(1\right)\)
cmtt: \(NH^2=NA.NC\left(2\right)\)
Ta lại có: \(HB.HC=AH^2=MN^2\)( 2 đường chéo bằng nhau) (3)
Xét \(\Delta MHN\) vuông tại H có
\(\Rightarrow MH^2+HN^2=MN^2=AH^2\left(4\right)\)
Từ (1),(2),(3) và (4) \(\Rightarrow HB.HC=MA.MB+NA.NC\left(đpcm\right)\)
c) Có \(HB=\frac{AC^2}{BC}\)
\(HC=\frac{AC^2}{BC}\)
\(\Rightarrow\frac{BH}{HC}=\frac{AB^2}{BC}:\frac{AC^2}{BC}=\frac{AB^2}{AC^2}=\left(\frac{AB}{AC}\right)^2\)
cảm ơn ạ