Cho tam giác ABC có góc A=100o ; Góc B-C=20o . Tính góc B và góc C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có:
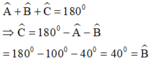
Suy ra ∆ABC cân tại A.

Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
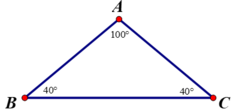

Ta có ∠C = 180o - 30o - 100o = 50o
Khi đó ∠(ACE) = 50o : 2 = 25o. Chọn D

Ta có ∠C = 180o - 30o - 100o = 50o
Khi đó ∠(ACE) = 50o : 2 = 25o. Chọn D

Ta có ∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 80o
Có ∠(ABO) + ∠(OBC) + ∠(BCO) + ∠(OCA) = 2.∠(OBC) + 2.∠(BCO) = 2(∠(OBC) + ∠(BCO)) = 80o
⇒ ∠(OBC) + ∠(BCO) = 40o ⇒ (BOC) = 140o. Ta có ∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 80o
Có ∠(ABO) + ∠(OBC) + ∠(BCO) + ∠(OCA) = 2.∠(OBC) + 2.∠(BCO) = 2(∠(OBC) + ∠(BCO)) = 80o
⇒ ∠(OBC) + ∠(BCO) = 40o ⇒ (BOC) = 140o. Chọn C
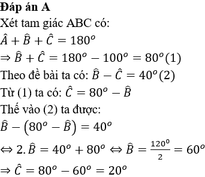
trong tam giác ta có
A+B+C=180
=> B+C=180-A=180-100=80
theo đề ta có hệ pt: \(\begin{cases}B+C=80\\B-C=20\end{cases}\)
<=> \(\begin{cases}B=50\\C=30\end{cases}\)
vậy B=50 dộ
C=30 độ
Xét \(\Delta ABC\) có:
\(\widehat {A} + \widehat {B} + \widehat {C} = 180^O\)(Định lí tổng 3 góc của 1 tam giác)
\(100^O + \widehat {B} + \widehat {C} = 180^O\)(\(\widehat {A} = 100^O (gt)\))
\(\widehat {B} + \widehat {C} = 180^O - 100^O\)
\(\widehat {B} + \widehat {C} = 80^O\) (1)
Mà \(\widehat {B} - \widehat {C} = 20^O\) (2)
Từ (1)(2), cộng vế với vế ta có:
\(2\widehat {B} = 100^O\)
\(\Rightarrow\)\(\widehat {B} = 100^O:2=50^O\)
\(\Rightarrow\)\(\widehat {C} = 50^O - 20^O = 30^O\)
Vậy \(\widehat {B} = 50^O; \widehat {C} = 30^O\)