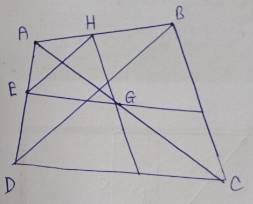
Cho tứ giác ABCD có \(F\in AC\) . Kẻ FE // CD (\(E\in AD\)); FG // BC (\(G\in AB\)). CM:
\(AF.BG=DE.AG\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: GE//CD
=>AG/AC=AE/AD
GH//BC
=>AG/AC=AH/AB
=>AE/AD=AH/AB
=>EH//BD
b: Vì EH//BD
nên AE/ED=AH/HB
=>AE*HB=AH*DE
a) Ta có: HG // BC (gt).
\(\Rightarrow\dfrac{AH}{HB}=\dfrac{AG}{AC}\) (1) (Định lý Ta - let).
Ta có: GE // CD (gt).
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AG}{AC}\) (2) (Định lý Ta - let).
Từ (1) và (2) \(\Rightarrow\dfrac{AE}{AD}=\dfrac{AH}{AB}.\)
\(\Rightarrow\) HE // BD.
b) Ta có: HE // BD (cmt).
\(\Rightarrow\dfrac{AE}{DE}=\dfrac{AH}{BH}\) (Định lý Ta - let).
\(\Rightarrow AE.BH=AH.DE\left(đpcm\right).\)

Các bước giải:
a) Vì EG // CD nên theo định lí Thalet ta có: \(\dfrac{AE}{AD}\) = \(\dfrac{AG}{AC}\)
Vì GH // CB nên theo định lí Thalet ta có: \(\dfrac{AG}{AC}\)= \(\dfrac{AH}{AB}\)
⇒ \(\dfrac{AG}{AC}\) = \(\dfrac{AH}{AB}\) ⇒ HE // BD (đpcm) (Thalet đảo)
b) HE // BD ⇒ \(\dfrac{AE}{AD}\) = \(\dfrac{AH}{AB}\)
⇒ \(\dfrac{AE}{AD-AE}\) = \(\dfrac{AH}{AB-AH}\)
⇒ \(\dfrac{AE}{DE}\) = \(\dfrac{AH}{BH}\)
⇒\(AE.BH=AH.DE\left(đpcm\right)\)

Các bước giải:
a) Vì EG // CD nên theo định lí Thalet ta có: \(\dfrac{AE}{AD}\) = \(\dfrac{AG}{AC}\)
Vì GH // CB nên theo định lí Thalet ta có: \(\dfrac{AG}{AC}\)= \(\dfrac{AH}{AB}\)
⇒ \(\dfrac{AG}{AC}\) = \(\dfrac{AH}{AB}\) ⇒ HE // BD (đpcm) (Thalet đảo)
b) HE // BD ⇒ \(\dfrac{AE}{AD}\) = \(\dfrac{AH}{AB}\)
⇒ \(\dfrac{AE}{AD-AE}\)= \(\dfrac{AH}{BH-AH}\)
⇒ \(\dfrac{AE}{DE}\) = \(\dfrac{AH}{BH}\)
⇒ AE.BH = AH.DE

A B C D E I F
THeo thales ta có
\(\Rightarrow\hept{\begin{cases}\frac{EF}{AB}=\frac{CE}{CA}\\\frac{EI}{CD}=\frac{AE}{AC}\end{cases}\Rightarrow}\frac{EF}{AB}+\frac{EI}{CD}=\frac{CE}{CA}+\frac{AE}{AC}=1\)VẬY ta có đpcm

A B C D E G F H
Xét tg ABC có
EF//AC (gt) (1)
EA=EB (gt)
=> FB=FC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và song song với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
EA=EB (gt); FB=FC (cmt) => EF là đường trung bình của tg ABC
\(\Rightarrow EF=\dfrac{1}{2}AC\) (2)
Xét tg BCD chứng minh tương tự ta cũng có GC=GD
Xét tg ADC có
GF//AC (gt) (3)
GC=GD (cmt)
=> HA=HD (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và song song với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
GC=GD (cmt); HA=HD (cmt) => GH là đường trung bình của tg ADC
\(\Rightarrow GH=\dfrac{1}{2}AC\) (4)
Từ (1) và (3) => EF//GH (cùng // với AC)
Từ (2) và (4) \(\Rightarrow EF=GH=\dfrac{1}{2}AC\)
=> EFGH là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
b/
Gọi O là giao của AC và BD
Ta có
FG//BD (gt); GH//AC (gt) \(\Rightarrow\widehat{HGF}=\widehat{DOC}\) (Góc có cạnh tương ứng vuông góc)
Để EFGH là Hình chữ nhật \(\Rightarrow\widehat{HGF}=90^o\)
\(\Rightarrow\widehat{HGF}=\widehat{DOC}=90^o\Rightarrow AC\perp BD\)
Để EFGH là hình chữ nhật => ABCD phải có 2 đường chéo vuông góc với nhau