Cho △DEF có DE = 6cm; DF = 8cm; EF= 10cm.
a. Chứng tỏ tam giác EDF vuông tại D.
b. Vẽ phân giác EI ( I ϵ DF ), từ I vẽ IH ⊥ EF ( H ϵ EF ). Chứng minh ID = IH
c. Gọi K là trung điểm của cạnh EF, đường thẳng KA cắt cạnh DF tại M. Tính MF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
28 tháng 9 2023
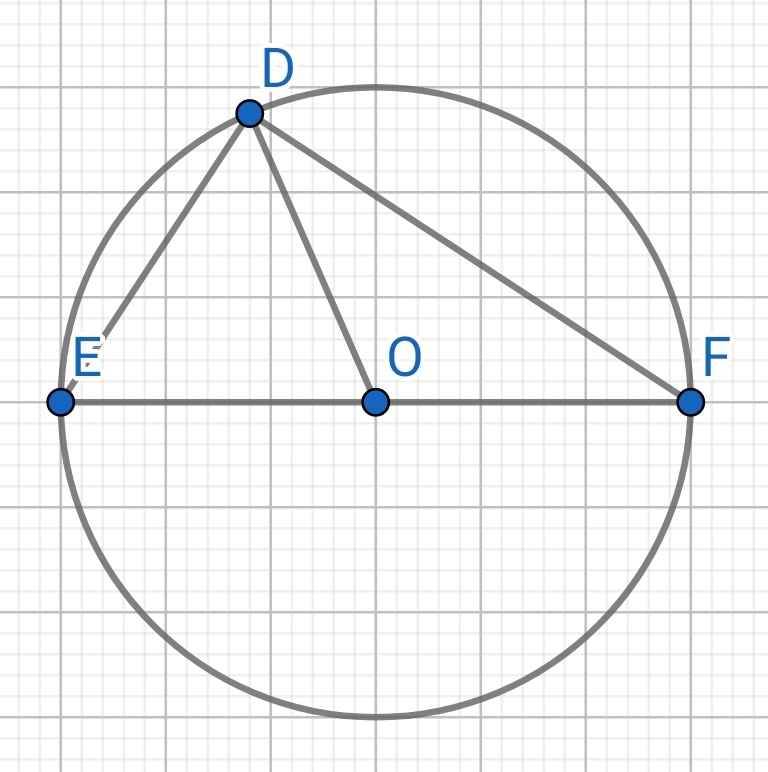Do EF đi qua O nên EF là đường kính của (O)
⇒ EF = 5.2 = 10 (cm)
Do ∆DEF nội tiếp (O) và EF là đường kính
⇒ ∆DEF vuông tại D
⇒ EF² = DE² + DF² (Pytago)
⇒ DF² = EF² - DE²
= 10² - 6²
= 64
⇒ DF = 8 (cm)
9 tháng 11 2016
Ta có: tam giác DEF = tam giác HIK
=> DE = HI ; EF = IK ; DF = HK
=> góc D = góc H
góc E = góc I
góc F = góc K
a/ Ta có: góc E = góc I (vì tam giác DEF = HIK)
Mà góc E = 400 => góc I = 400
b/ Chu vi tam giác DEF= chu vi tam giác HIK
= DE + EF + HK = DE+EF+DF=2+5+6=13 (cm)
Vậy chu vi tam giác DEF = chu vi tam giác HIK = 13 cm
nhớ cho mik nha =)
13 tháng 11 2021
Ta có:
ΔABC=ΔDEF\(\Rightarrow\left\{{}\begin{matrix}AB=DE\\BC=EF\\AC=DF\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AB+DE=10\left(cm\right)\\EF=6\left(cm\right)\\AC=7\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{10}{2}=5\left(cm\right)\\BC=6\left(cm\right)\\AC=7\left(cm\right)\end{matrix}\right.\)
Chu vi ΔABC là:
\(C_{ABC}=AB+BC+AC=5+6+7=18\left(cm\right)\)
2 tháng 4 2021
Xét ΔDEF có DK là đường phân giác ứng với cạnh EF(gt)
nên \(\dfrac{KE}{KF}=\dfrac{DE}{DF}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{KE}{KF}=\dfrac{27}{9}=3\)
2 tháng 4 2021
Ta có: \(\dfrac{KE}{KF}=3\)(cmt)
\(\Leftrightarrow KE=3\cdot KF=3\cdot6=18\left(cm\right)\)
Vậy: KE=18cm
18 tháng 3 2023
a: \(EF=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xet ΔEDF có EK là phân giác
nên DK/DE=FK/FE
=>DK/3=FK/5=(DK+FK)/(3+5)=8/8=1
=>DK=3cm; FK=5cm
b: Xet ΔDEK vuông tại D và ΔHEI vuông tại H có
góc DEK=góc HEI
=>ΔDEK đồng dạng với ΔHEI
=>ED/EH=EK/EI
=>ED*EI=EK*EH
c: góc DKI=90 độ-góc KED
góc DIK=góc HIE=90 độ-góc KEF
mà góc KED=góc KEF
nên góc DKI=góc DIK
=>ΔDKI cân tại D
mà DG là trung tuyến
nên DG vuông góc IK
H9
HT.Phong (9A5)
CTVHS
27 tháng 8 2023
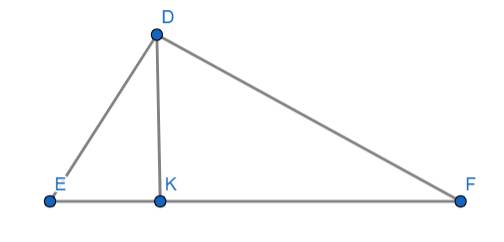
Xét ta có:
\(EF^2=7,5^2=56,25\left(cm\right)\) (1)
Mà: \(DF^2+DE^2=4,5^2+6^2=56,25\left(cm\right)\) (2)
Từ (1) và (2) ta có:
\(EF^2=DE^2+DF^2\)
\(\Rightarrow\Delta DEF\) vuông tại D có đường cao DK
a) Áp dụng hệ thức hai cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{DK^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Rightarrow DK^2=\dfrac{DE^2DF^2}{DF^2+DF^2}\Rightarrow DK=\sqrt{\dfrac{DE^2DF^2}{DF^2+DE^2}}\)
\(\Rightarrow DK=\sqrt{\dfrac{4,5^2\cdot6^2}{4,5^2+6^2}}=3,6\left(cm\right)\)
b) Áp dụng hệ thức hình chiếu và cạnh góc vuông ta có:
\(\left\{{}\begin{matrix}DE^2=EF\cdot EK\\DF=EF\cdot FK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{DE^2}{EF}\\FK=\dfrac{DF^2}{EF}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{6^2}{7,5}=4,8\left(cm\right)\\FK=\dfrac{4,5^2}{7,5}=2,7\left(cm\right)\end{matrix}\right.\)
27 tháng 8 2023
a: Xét ΔDEF có EF^2=DE^2+DF^2
nên ΔDEF vuông tại D
Xét ΔDEF vuông tại D có DK là đường cao
nên DK*FE=DE*DF
=>DE*7,5=27
=>DE=3,6cm
b: ΔDEF vuông tại D có DK là đường cao
nên EK*EF=ED^2
=>EK=6^2/7,5=4,8cm
FK=7,5-4,8=2,7cm
a: Xét ΔEDF có \(EF^2=ED^2+DF^2\)
nen ΔEDF vuông tại D
b: Xét ΔEDI vuông tại D và ΔEHI vuông tại H có
EI chung
góc DEI=góc HEI
Do đó: ΔEDI=ΔEHI
Suy ra: ID=IH