Cho tam giác ABC : BE là phân giác của góc ABC ; CF là phân giác của ACB . Gọi I là giao điểm của BE và CF
Chứng minh rằng Góc BIC = 90 độ + góc BAC : 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2023
a: Xét ΔABD vuông tại A và ΔABE vuông tại A có
AB chung
AD=AE
=>ΔABD=ΔABE
=>BD=BE
=>ΔBED cân tại B
mà góc BED=60 độ
nên ΔBED đều
c: góc DBC=góc DBA+góc CBA
=30+60=90 độ
=>BD vuông góc BC
b: Sửa đề: Cm EB=EC
Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
=>EB=EC
29 tháng 12 2021
a: Xét ΔAEB vuông tại E và ΔADC vuông tại D có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAEB=ΔADC
TT
0
KV
10 tháng 12 2023
Sửa đề:
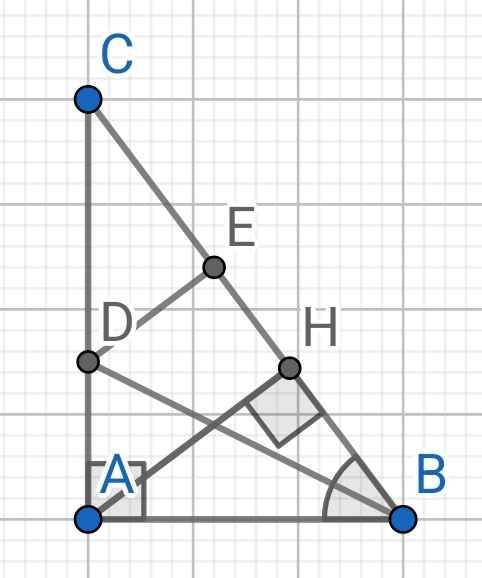
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BA = BE. BD là tia phân giác của góc ABC, AH vuông góc với BC. Chứng minh:
a, Tam giác ABD = tam giác EBD
b, AH // DE
Giải
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
BD là cạnh chung
∠ABD = ∠EBD (cmt)
BA = BE (gt)
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BC
Mà AH ⊥ BC (gt)
⇒ AH // DE
10 tháng 12 2023
Để chứng minh a, ta cần chứng minh hai tam giác ABD và EBD có cạnh và góc tương ứng bằng nhau.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì BA = BE, và góc ABD = góc DBC, nên ta có hai cạnh và góc tương ứng bằng nhau, theo nguyên tắc cạnh-góc-cạnh (SAS), ta có tam giác ABD = tam giác EBD.
Để chứng minh b, ta cần chứng minh hai đường thẳng AH và DE là song song.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì tam giác ABD = tam giác EBD (đã chứng minh ở câu a), nên ta có góc ADB = góc EDB.
Vì góc ADB = góc EDB và góc ABD = góc DBC, nên theo nguyên tắc góc tương đương, ta có AH // DE.
Vậy, ta đã chứng minh được cả hai phần a và b.
PS
0
HT
0
K là giao điêm của AI;BC
BIK=IBA+IAB
CIK=IBC+ICB
=> BIC=BIK+CIK=IBA+IAB+ICB+IBC
=90+BAC/2