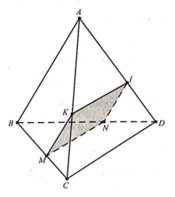
Cho tứ diện ABCD có AB=6; CD=8. Cắt tứ diện bởi một mặt phẳng song song với AB, CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng
A. 31 7
B. 18 7
C. 24 7
D. 15 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
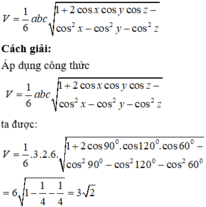

Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
![]()
Cách giải:
Áp dụng công thức ![]()
ta được: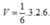
![]()
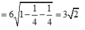
Chọn D.

Đán án C
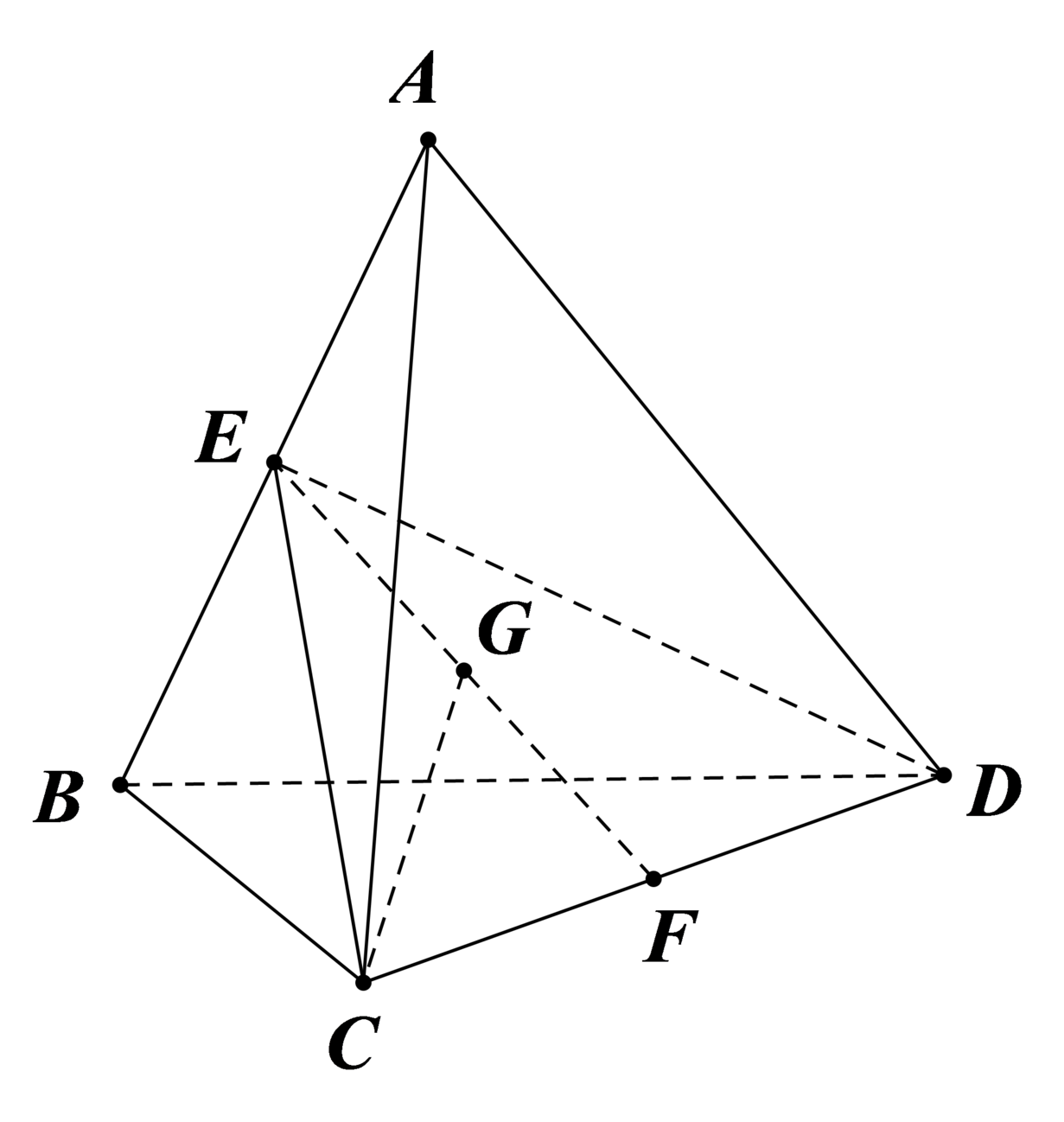
Gọi G là trung điểm của EF thì G chính là tâm mặt cầu ngoại tiếp tứ diện.
Ta có C E 2 = C B 2 + C A 2 2 − A B 2 4 = 6 2 + 6 2 2 − 2 2 4 = 35 ,
E F 2 = C E 2 − C F 2 = 35 − 2 2 = 31
⇒ G F = 31 2 ⇒ R = G C = G F 2 + C F 2 = 31 4 + 4 = 47 2 .
Vậy diện tích mặt cầu cần tính là:
S = 4 π R 2 = 4 π . 47 4 = 47 π .

Chọn đáp án C.
Giả sử một mặt phẳng song song với AB và CD cắt tứ diện ABCD theo một thiết diện là hình thoi MNIK như hình vẽ trên.
Khi đó ta có: 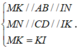

Đáp án B.
Phương pháp
Gọi E và F lần lượt là trung điểm của AC và CD, chứng minh
E
F
⊥
A
B
E
F
⊥
C
D
.
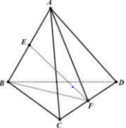
Cách giải
Gọi E và F lần lượt là trung điểm của AC và CD ta có:
Δ A C D = Δ B C D c . c . c ⇒ A F = B F ⇒ Δ A B F
cân tại F ⇒ E F ⊥ A B .
Chứng minh tương tự ta có
E F ⊥ C D ⇒ d A B ; C D = E F .
Ta có:
A F = 6 3 2 = 3 3
Xét tam giác vuông AEF có
E F = A F 2 − A E 2 = 3 2