Cho tam giác ABC có AB=AC=4a; BC=2a. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
DT
1
S
0

PT
0

NM
1

AH
Akai Haruma
Giáo viên
16 tháng 9 2023
Lời giải:
$|\overrightarrow{BC}|=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$ theo định lý Pitago.
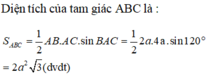
 Chúc bạn học tốt
Chúc bạn học tốt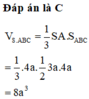
Gọi (O;R) là đt ngoại tiếp tam giác ABC
Gọi D là gđ của AO và đt (O)
Kẻ đường cao AH => AH vừa là đường cao, đồng thời là đường trung tuyến
ÁP dụng định lí pytago vào tam giác AHB vuông tại H có:\(AH=\sqrt{AB^2-BH^2}=\sqrt{\left(4a\right)^2-\dfrac{BC^2}{4}}\)\(=\sqrt{16a^2-a^2}=a\sqrt{15}\)
Chứng minh được: \(\Delta AHB\sim ACD\left(g.g\right)\)
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{AD}\) \(\Leftrightarrow AD=\dfrac{AB.AC}{AH}=\dfrac{4a.4a}{a\sqrt{15}}=\dfrac{16a\sqrt{15}}{15}\)
\(\Rightarrow R=\dfrac{AD}{2}=\dfrac{8a\sqrt{15}}{15}\)