Mp xOy, tam giác ABC; BC=2AB. đường trùn tuyến xuất phát từ B d:x+y-2=0 Biết \(\widehat{ABC}=120\) và A(3;1). Tìm tọa độ B, C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)


XÉT\(\Delta OMN\)VÀ \(\Delta MPO\) CÓ
OM LÀ CẠNH CHUNG
GÓC N= GÓC P =90*
O1=O2 VÌ OM LÀ TIA P/G CỦA GÓC O
=>\(\Delta OMN\)=\(\Delta OPM\)(GCG)
B;VÌ TAM GIÁC OMN=TAM GIÁC OMP
=>ON=OP (cạnh tương ứng)
c;

câu a sai đề rồi bn
hok tốt
phải là tam giác OMQ = tam giác OPN chứ

a: Xét ΔOPM vuông tại P và ΔONM vuông tại N có
OM chung
\(\widehat{POM}=\widehat{NOM}\)
Do đó; ΔOPM=ΔONM
b: Ta có: ΔOPM=ΔONM
nên MN=MP
hay ΔMNP cân tại M
mà \(\widehat{NMP}=60^0\)
nên ΔMNP đều
c: Ta có: ON=OP
MN=MP
Do đó: OM là đường trung trực của NP
hay OM vuông góc tới NP tại Q

Đáp án là A
![]()
![]()
![]()
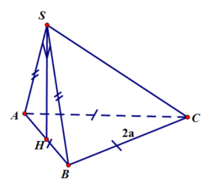
Ta có :
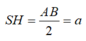
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là

Vậy thể tích khối chóp SABC là:
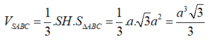

a: A(-1;2); B(1;3); C(2;1)
Tọa độ của vecto CA là:
\(\left\{{}\begin{matrix}x=-1-2=-3\\y=2-1=1\end{matrix}\right.\)
Vậy: \(\overrightarrow{CA}=\left(-3;1\right)\)
Tọa độ vecto BC là:
\(\left\{{}\begin{matrix}x=2-1=1\\y=1-3=-2\end{matrix}\right.\)
Vậy: \(\overrightarrow{BC}=\left(1;-2\right)\)
b: tọa độ trọng tâm G của ΔABC là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+1+2}{3}=\dfrac{2}{3}\\y=\dfrac{2+3+1}{3}=2\end{matrix}\right.\)
c: \(A\left(-1;2\right);B\left(1;3\right);C\left(2;1\right)\)
\(AB=\sqrt{\left(1+1\right)^2+\left(3-2\right)^2}=\sqrt{1^2+2^2}=\sqrt{5}\)
\(AC=\sqrt{\left(2+1\right)^2+\left(1-2\right)^2}=\sqrt{3^2+1^2}=\sqrt{10}\)
\(BC=\sqrt{\left(2-1\right)^2+\left(1-3\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=\sqrt{5}+\sqrt{5}+\sqrt{10}=2\sqrt{5}+\sqrt{10}\)
Vì \(AB^2+BC^2=AC^2\)
nên ΔABC vuông tại B
=>\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC=\dfrac{1}{2}\cdot\sqrt{5}\cdot\sqrt{5}=\dfrac{5}{2}\)
Lời giải:
Gọi trung điểm $AC$ là $M$.
Theo định lý cos:
$\cos B=\frac{a^2+c^2-b^2}{2ac}$. Mà theo đề thì $a=2c$ nên:
$\frac{-1}{2}=\cos 120^0=\frac{5c^2-b^2}{4c^2}$
$\Rightarrow b^2=7c^2$
Theo định lý đường trung tuyến:
$BM^2=\frac{c^2+a^2}{2}-\frac{b^2}{4}=\frac{c^2+4c^2}{2}-\frac{7c^2}{4}=\frac{3}{4}c^2$
$AM^2=(\frac{b}{2})^2=\frac{7}{4}c^2$
Từ những số tính toán ở trên suy ra:
$c^2+\frac{3}{4}c^2=\frac{7}{4}c^2\Leftrightarrow AB^2+BM^2=AM^2$ nên theo định lý Pitago đảo thì $ABM$ vuông tại $B$
$\Rightarrow \overrightarrow{u_{AB}}=\overrightarrow{n_{BM}}=(1,1)$
$\Rightarrow \overrightarrow{n_{AB}}=(1,-1)$
PTĐT $AB$: $(x-3)-(y-1)=0\Leftrightarrow x-y-2=0$
$B$ vừa thuộc đt $x+y-2=0$ vừa thuộc ĐT $x-y-2=0$ nên dễ tính $B(2,0)$
---------------------
Gọi tọa độ $C$ là $(t,t')$ thì tọa độ $M$ là $(\frac{3+t}{2}; \frac{t'+1}{2})$
Vì $M\in (x+y-2=0)$ nên: $\frac{3+t}{2}+\frac{t'+1}{2}=0\Leftrightarrow t'=-t$
Theo đề:
$a=2c\Leftrightarrow a^2=4c^2\Leftrightarrow (t-2)^2+(-t)^2=4[(3-2)^2+(1-0)^2]$
$\Leftrightarrow t=1\pm\sqrt{3}$
Vậy............