Cho tứ diện ABCD có DA ⊥ (ABC), tam giác ABC cân tại A với AB=AC=a; BC=\(\dfrac{6a}{5}\). Gọi M là trung điểm của BC, kẻ AH ⊥ MD, với H thuộc MD.
a) Chứng minh rằng AH ⊥ (BCD)
b) Cho AD=\(\dfrac{4a}{5}\) Tính góc giữa hai đường thẳng AC và DM.
c) Gọi G1 ; G2 là trọng tâm các tam giác ABC và DBC. Chứng minh rằng G1G2 ⊥ (ABC).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

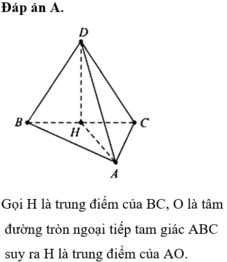
Đáp án A
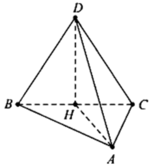
Gọi H là trung điểm của BC, O là tâm đường tròn ngoại tiếp tam giác ABC suy ra H là trung điểm của AO.
Ta có D H = 3. V A B C D S Δ A B C = a 3 4 .
Gọi J là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Khi đó J O ⊥ A B C .
Do J A = R , O A = a nên J O = R 2 − a 2 .
Mặt khác H O ⊥ J O , H O ⊥ H D nên ta có
a 3 4 ± R 2 − a 2 2 + a 2 2 = R 2 ⇔ R = a 91 8 .

a: Xét tứ giác AHCE có
D là trung điểm chung của AC và HE
góc AHC=90 độ
Do đó: AHCE là hình chữ nhật
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
=>BC=2*BH=6cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot4=2\cdot6=12\left(cm^2\right)\)

Tương tự 2B. Ta chứng minh được ABCD là hình thang vuông. Từ đó tính được diện tích ABCD là:
S A B C D = s A B C + s A C D = 1 2 A C . A B + 1 2 C A . D H = 1 2 .4.4 + 1 2 .4.2 = 12 c m 2
(Với DH là đường cao tam giác ACD)

Gọi chiều cao AH là x :
Áp dụng công thức tính diện tích tam giác ta được :
\(\frac{1}{2}\).BC.AH = 120
\(\frac{1}{2}\).20.x =120
10x =120
x = 12
=) AH = 12 cm
b) Xét tam giác ABC có :
M là trung điểm của AB
N là trung điểm của AC
=) MN là đường trung bình của tam giác ABC
=) MN // BC ; MN=\(\frac{1}{2}\)BC
Xét tứ giác BMNC có
MN // BC
=) Tứ giác BMNC là hình thanh
Giả sử MN cắt AH tại K
Xét tam giác ABH có :
M là trung điểm của AB
MK // BH
=) K là trung điểm của AH
Do K là trung điểm của AH
=) AK=KH=\(\frac{AH}{2}\)=\(\frac{12}{2}\)=6
Ta có MN=\(\frac{BC}{2}\)=10
Diện tích hình thang BMNC là
\(\frac{1}{2}\).KH.(MN+BC)= \(\frac{1}{2}\).6.(10+20)
= 90 cm2
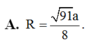
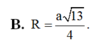
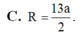


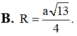
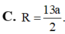

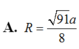


Do ABC cân \(\Rightarrow AM\perp BC\)
Mà \(DA\perp\left(ABC\right)\Rightarrow DA\perp BC\)
\(\Rightarrow BC\perp\left(ADM\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(BCD\right)\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}MN||AC\\MN=\dfrac{1}{2}AC=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(AC;DM\right)}=\widehat{\left(MN;DM\right)}=\widehat{DMN}\)
\(DN=\sqrt{AD^2+AN^2}=\sqrt{AD^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{a\sqrt{89}}{10}\)
\(AM=\sqrt{AB^2-\left(\dfrac{BC}{2}\right)^2}=\dfrac{4a}{5}\Rightarrow DM=\sqrt{AD^2+AM^2}=\dfrac{4a\sqrt{2}}{5}\)
Định lý hàm cos cho tam giác DMN:
\(cos\widehat{DMN}=\dfrac{DM^2+MN^2-DN^2}{2DM.MN}=\dfrac{2\sqrt{2}}{5}\)
\(\Rightarrow\widehat{DMN}\approx55^033'\)
c.
M là trung điểm BC nên hiển nhiên \(G_1\) nằm trên AM và \(G_2\) nằm trên DM
Do \(G_1\) là trọng tâm ABC \(\Rightarrow\dfrac{AG_1}{AM}=\dfrac{2}{3}\Rightarrow\dfrac{MG_1}{AM}=\dfrac{1}{3}\)
Do \(G_2\) là trọng tâm DBC \(\Rightarrow\dfrac{DG_2}{DM}=\dfrac{2}{3}\Rightarrow\dfrac{MG_2}{DM}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{MG_1}{AM}=\dfrac{MG_2}{DM}\Rightarrow G_1G_2||DA\) (Talet đảo)
Mà \(DA\perp\left(ABC\right)\Rightarrow G_1G_2\perp\left(ABC\right)\)