Cho \(\Delta\)ABC vuông tại A. D\(\in\)cạnh huyền BC sao cho CA=CD ; AH là đường cao. Lấy E\(\in\)AB sao cho AE=AH. CM : AD vuông góc với EH; DE vuông góc với AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2023
a: góc BAD+góc CAD=90 độ
góc HAD+góc CDA=90 độ
góc CAD=góc CDA
=>góc BAD=góc HAD
ΔAHE cân tại A
mà AD là phân giác
nên AD vuông góc EH
b: Xét ΔAED và ΔAHD có
AE=AD
góc EAD=góc HAD
AD chung
=>ΔAED=ΔAHD
=>góc AED=góc AHD=90 độ
=>DE vuông góc AB
29 tháng 1 2022
c: Xét ΔCDA có CH là đường phân giác
nên CH/HA=CD/HD
mà CH>CD
nên HA>HD
4 tháng 3 2022
a, Xét tam giác ACH và tam giác ECH
CH _ chung ; AC = CE ; ^ACH = ^ECH
Vậy tam giác ACH = tam giác ECH (c.g.c)
4 tháng 3 2022
a: Xét ΔCHA và ΔCHE có
CA=CE
\(\widehat{ACH}=\widehat{ECH}\)
CH chung
Do đó: ΔCHA=ΔCHE
b: Xét ΔCAD và ΔCED có
CA=CE
\(\widehat{ACD}=\widehat{ECD}\)
CD chung
Do đó:ΔCAD=ΔCED
Suy ra: DA=DE và \(\widehat{CAD}=\widehat{CED}=90^0\)
Ta có: DA=DE
mà DE<DB
nên DA<DB
D
29 tháng 1 2022
- Gợi ý:
Câu 1:
a) - Sửa lại đề: Tam giác ABD=Tam giác ICE (c-g-c) do có AB=AC=CI, góc ABC=góc ACB=góc ECI, BD=CE.
b) Do tam giác ABD=Tam giác ICE nên AD=IE :
AE+EI>AI=2AC=AB+AC
=>AE+AD>AB+AC.
Câu 2:
- Tam giác MBD=Tam giác NCE do góc MDB=góc CEN=900, BD=CE,
góc MBD=góc NCE. nên BM=CN
Câu 3:
- AB=AM+BM ; CI=CN+NI.
=>AM=NI.
=>AM+AN=AM+NI=AI=AB+AC.
-c/m MN>BC (c/m mệt lắm nên mình nói ngắn gọn).
MN cắt BC tại F =>MF>DF, NF>EF
MF+NF>DF+EF=DF+CF+CE=DF+CF+BD=BC =>MN>BC
20 tháng 2 2022
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Xét ΔKBD và ΔKCE có
\(\widehat{KBD}=\widehat{KCE}\)
BD=CE
\(\widehat{KDB}=\widehat{KEC}\)
Do đó:ΔKBD=ΔKCE
KV
11 tháng 7 2023
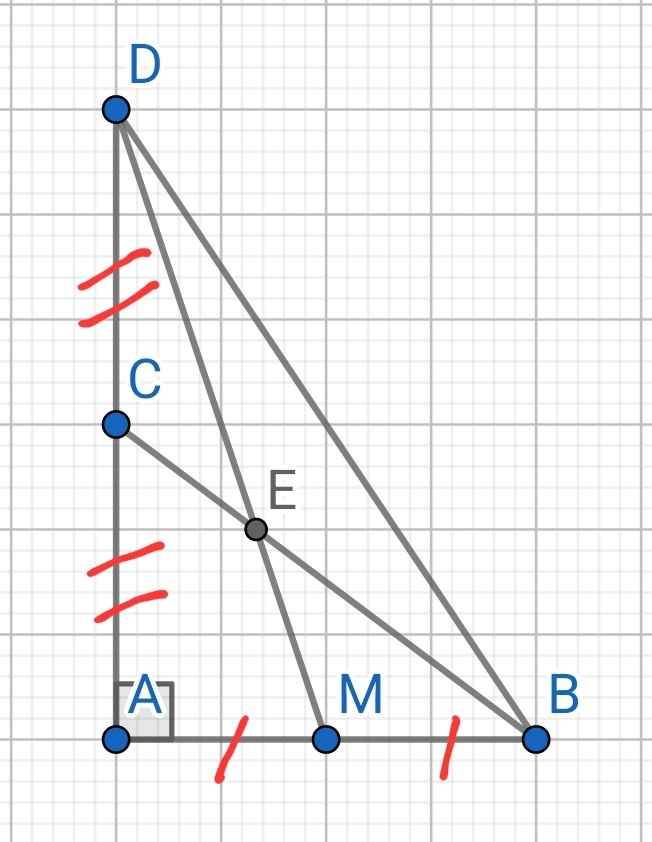
Do CA = CD nên C là trung điểm của AD
Xét ∆ABD có:
C là trung điểm của AD
⇒ BC là đường trung tuyến ứng với cạnh AD (1)
Lại có M là trung điểm AB (gt)
⇒ DM là đường trung tuyến ứng với cạnh AB (2)
Từ (1) và (2) ⇒ E là trọng tâm của ∆ABD
⇒ BE = 2/3 BC = 2/3 . 10 = 20/3 (cm)