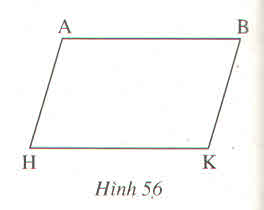
Cho hình bên, trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK; AH = BK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
3
2 tháng 6 2017
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
DT
1 tháng 12 2017
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................
13 tháng 8 2023
a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
=>ΔAHD=ΔBKC
b: Xét tứ giác ABKH có
AB//KH
AH//BK
=>ABKH là hình bình hành
=>AB=KH
19 tháng 4 2020
a. Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠(M') = ∠A2(sole trong)
∠A1= ∠A2(gt)
⇒ ∠(M') = ∠A1nên ΔADM' cân tại D
* DM là phân giác của ∠(ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠(N') = ∠B1nên ΔBCN' cân tại C.
* CN là phân giác của ∠(BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ PN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN = M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
b)MN=AB+M′N′/2 (tính chất đường trung bình của hình thang)
⇒MN=AB+M′D+CD+CN′/2(1)
Mà M′D=AD,CN′=BC. Thay vào (1)
MN=AB+AD+CD+BC/2=a+d+c+b/2
Nối AK, ta có:
AB // HK (giả thiết)
⇒ ∠(A1 ) =∠(K1 ) (hai góc so le trong)
+) Lại có: AH // BK (giả thiết)
⇒ ∠ (A2 ) = ∠(K2 ) (hai góc so le trong)
Xét ΔABK và ΔKHA, ta có:
∠(A1 ) =∠(K1 ) ( chứng minh trên)
AK cạnh chung
∠(K2 ) =∠(A2 ) (chứng minh trên)
Suy ra: ΔABK =ΔKHA (g.c.g)
Vậy: AB = KH; BK = AH ( 2 cạnh tương ứng)