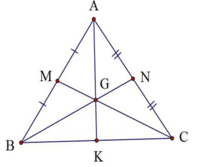
Tam giác ABC, MA=MB, NA=NC. CM cắt Bn tại G; AG cắt BC tại K. Chứng minh KB = KC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2021
a) Xét ΔABC có
AM là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{MB}{MC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
Xét ΔABC có
BN là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{NC}{NA}=\dfrac{BC}{AB}\)(Tính chất đường phân giác của tam giác)
Xét ΔABC có
CP là đường phân giác ứng với cạnh AB(gt)
nên \(\dfrac{PA}{PB}=\dfrac{AC}{BC}\)(Tính chất đường phân giác của tam giác)
Ta có: \(\dfrac{MB}{MC}\cdot\dfrac{NC}{NA}\cdot\dfrac{PA}{PB}\)
\(=\dfrac{AB}{AC}\cdot\dfrac{BC}{AB}\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB\cdot AC\cdot BC}{AB\cdot AC\cdot BC}=1\)(đpcm)
AH
Akai Haruma
Giáo viên
19 tháng 1 2021
Lời giải:
Ta có:
\(\frac{MB}{MC}=\frac{S_{BIM}}{S_{CIM}}=\frac{S_{BAM}}{S_{CAM}}=\frac{S_{BAM}-S_{BIM}}{S_{CAM}-S_{CIM}}=\frac{S_{BAI}}{S_{CAI}}\)
\(\frac{NC}{NA}=\frac{S_{BNC}}{S_{BAN}}=\frac{S_{CNI}}{S_{ANI}}=\frac{S_{BNC}-S_{CNI}}{S_{BAN}-S_{ANI}}=\frac{S_{BIC}}{S_{BAI}}\)
\(\frac{PA}{PB}=\frac{S_{PAC}}{S_{PBC}}=\frac{S_{PAI}}{S_{PBI}}=\frac{S_{PAC}-S_{PAI}}{S_{PBC}-S_{PBI}}=\frac{S_{PAI}}{S_{BIC}}\)
Nhân 3 đẳng thức với nhau:
\(\frac{MB}{MC}.\frac{NC}{NA}.\frac{PA}{PB}=1\) (đpcm)
14 tháng 9
a: Xét ΔDAB có DM là phân giác
nên \(\frac{MB}{MA}=\frac{DB}{DA}\) (1)
b: Xét ΔDAC có DN là phân giác
nên \(\frac{NC}{NA}=\frac{DC}{DA}\)
mà DC=DB
nên \(\frac{NC}{NA}=\frac{DB}{DA}\) (2)
Từ (1),(2) suy ra \(\frac{MB}{MA}=\frac{NC}{NA}\)
c: Sửa đề: Chứng minh MN//BC
Xét ΔABC có \(\frac{MB}{MA}=\frac{NC}{NA}\)
nên MN//BC
Theo bài ra ta có diện tích ABG=ACG; Vì hai tam giác ABG và ACG có cạnh AG chung nên đường cao hạ từ B và đường cao hạ từ C sẽ bằng nhau ( *)
- Xét tam giác BGK và CGK có cạnh GK chung và từ (*) ta có đường cao hạ từ B và C bằng nhau. Do đó: Diện tích BGK và CGK bằng nhau (**)
Mặt khác ta thấy: hai tam giác BGK và CGK có chung đường cao hạ từ G (***)
- Từ ( **) và (***) ta có KB=KC ( đpcm)