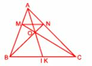
Cho tam giác ABC, gọi các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho AB= 3 x AM; AC= 3 x AN.
a) So sánh diện tích tam giác MBC và diện tích tam giác NCB.
b) So sánh MN với Bc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 12 2018
a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.
NH
8 tháng 1 2020
\(S_{AMC}=\frac{1}{3}S_{ABC}\) ( Vì hai tam giác có chung chiều cao hạ từ đỉnh \(C\)xuống \(AB\) và \(AM=\frac{1}{3}AB\))
\(S_{BNC}=\frac{1}{3}S_{ABC}\) ( Vì hai tam giác có chung chiều cao hạ từ đỉnh \(B\)xuống \(AC\) và \(NC=\frac{1}{3}AC\))
\(S_{ABP}=\frac{1}{3}S_{ABC}\) ( Vì hai tam giác có chung chiều cao hạ từ đỉnh \(A\)xuống \(BC\)và \(BP=\frac{1}{3}BC\))
Suy ra : \(S_{AMC}+S_{BNC}+S_{BKP}=S_{ABC}\)
Tuy nhiên trên hình vẽ tổng diện tích 3 tam giác chưa phủ kín \(S_{ABC}\) , còn phần trống là \(S_{IHK}\).
Mà trong tổng diện tích 3 tam giác trên có : \(S_{AMH}\) ; \(S_{BKP}\); \(S_{INC}\) bị tính 2 lần .
Vậy : \(S_{IHK=}S_{AMH}+S_{BKP}+S_{INC}\)( đpcm )
6 tháng 2 2022
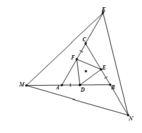
a: Xét ΔBAC có
AD/AB=AE/AC(2)
nên DE//BC
b: Xét ΔABM có DN//BM
nên DN/BM=AD/AB(1)
Xét ΔACM có NE//MC
nên NE/MC=AE/AC(3)
Từ (1), (2) và (3) suy ra DN/BM=NE/MC
=>DN/NE=5/2
hay DN=2,5NE
minh ? minh ?