Cho hình vẽ-: Biết OA = OB ; AC = BC. Chứng minh OC là tia phân giác của góc AOB O A C B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
0
CM
21 tháng 8 2017
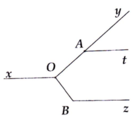
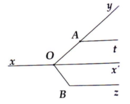
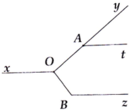
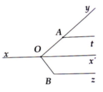Kẻ tia đối Ox' của Ox =>
y
O
x
'
^
= 40°
=> y O x ' ^ = y A t ^ (hai góc đồng vị bằng nhau)
=> Ox' // At (1).
Mặt khác: OA ⊥ OB => A O B ^ = 90 °
=> x ' O B ^ = y O B ^ − y O x ' ^ = 90 ° − 40 ° = 50 °
=> x ' O B ^ = O B z ^ = 50 ° + 130 ° = 180 °
(hai góc trong cùng phía bù nhau)
=>Ox' //Bz (2).
Từ (1) và (2), suy ra At //Bz
VT
24 tháng 3 2017
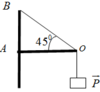
Ta có P = mg = 6.10=60 (N)
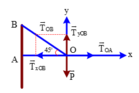
Biểu diễn các lực như hình vẽ
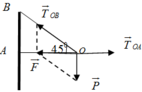
Theo điều kiện cân bằng
T → O B + T → O A + P → = 0 ⇒ F → + T → O A = 0
⇒ F → ↑ ↓ T → O A F = T O A
Góc α là góc giữa OA và OB: α= 45 0
S i n 45 0 = P T O B ⇒ T O B = 60 S i n 45 0 = 60 2 ( N )
C o s α = F T O B = T O A T O B ⇒ T O A = T O B . C o s 45 0 = 60 2 . 2 2 = 60 ( N )
VT
20 tháng 11 2018
Chọn đáp án A
? Lời giải:
Cách 1:
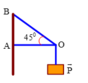
Biểu diễn các lực như hình vẽ
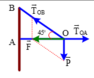
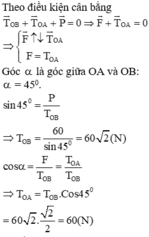
Cách 2:
Chọn hệ quy chiếu Oxy như hình vẽ.
16 tháng 12 2021
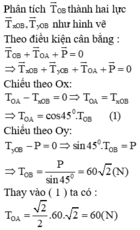
cho em hỏi là tại sao lực căng dây T_OB lại hướng vào B trong khi đó lực T_OA lại hướng ra ngoài vậy ạ. Và trong trường hợp đó thì lực F là lực gì vậy ạ?
HP
13 tháng 12 2021
a. Xét \(2\Delta\): \(\Delta AOC\) và \(\Delta BOC\) có:
\(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\AC=BC\left(gt\right)\\OC.chung\end{matrix}\right.\)
\(\Rightarrow\Delta AOC=\Delta BOC\left(c.c.c\right)\)
b. Theo câu a, suy ra:
\(\widehat{OAC}=\widehat{OBC}\)
Mà: \(\widehat{OAC}=110^o\)
\(\Rightarrow\widehat{OBC}=110^o\)
CT
0
30 tháng 9 2021
Ta có OA vuông góc với OB' nên AOB' = 90o.
- OA' vuông góc với OB nên A'OB = 90o
=> AOB + AOA' = A'OB
Mà AOB = 60O, A'OB = 90O
=> 60O + AOA' = 90O
AOA' = 90O - 60O = 30O
=> AOA' + AOB' = A'OB'
Mà AOA' = 30O, AOB' = 90O
=> 30O + 90O = A'OB'
=> A'OB' = 120O
Hình mk vẽ hơi xấu bạn nhé
Học tốt nha bạn
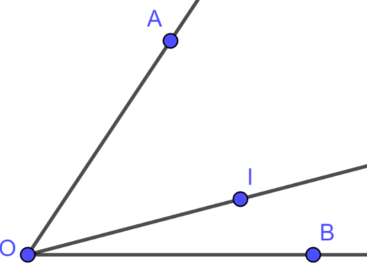
- Xét \(\Delta OAC\) và \(\Delta OBC\) có:
OA = OB ( gt ) (2 cạnh tương ứng )
AC = BC ( gt ) (2 cạnh tương ứng )
OC cạnh chung (2 cạnh tương ứng )
\(\Rightarrow\Delta AOC=\Delta BOC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AOC}=\widehat{BOC}\) mà OC nằm giữa OA và OB
=> OC là tia phân giác của \(\widehat{AOB}\)