Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH.
a. Tính BC.
b. Chứng minh AB2 = BH.BC
c. Tính BH; HC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
2
16 tháng 3 2022
vì trong tam giác vuông tại A nên =>AB=AC;B=C
vì AB=AC(cmt)=>AC=6cm
còn BC thì thì tui chịu
NN
16 tháng 3 2022
TK:
Định lí pi-ta-go
Ta giác ABC vuông tại A=> AB và AC là cạnh góc vuông còn BC là cạnh huyền
=>AB2+AC2=BC2
hay 62+82=BC2
=>100=BC2
=>BC2=102
=>BC=10cm
CM
18 tháng 9 2018
Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
19 tháng 1 2022
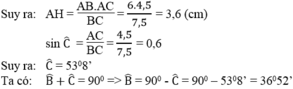
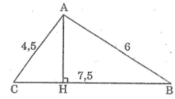
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=\left(BC-CH\right)BC\)
\(\Rightarrow36=\left(7,5-CH\right)7,5=56,25-7,5CH\)
\(\Leftrightarrow CH=\dfrac{27}{10}\)cm
NN
3
22 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
13 tháng 4 2021
b) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{HBA}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
BD) 
DBCD.
6 tháng 4 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
b) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)
14 tháng 2 2022
a: BC=10cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC∼ΔHBA
c: AH=4,8cm
BH=3,6cm
CH=6,4cm
a ΔABC vuông ở A
⇒Góc A= 90 độ
Áp dụng định lý Pitago vào ΔABC:
BC²=AB²+AC²
BC²=6²+8²
BC²=100
⇒BC=10 cm
b AB/HB=BC/BA
=> AB2=HB×BC
⇒HB=AB²/BC
⇒HB=6²/10=3,6(cm)
Tương tự: AC²=HC×BC
⇒HC=AC²/BC
⇒HC=8²/10=6,4(cm)
Vậy BH=3,6 cm và HC=6,4 cm