Phần tự luận
Nội dung câu hỏi 1
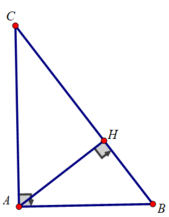
Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH
a) Tính BC, AH, ∠B ; ∠C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC có:
A B 2 + A C 2 = 6 2 + 8 2 = 100 = B C 2
Tam giác ABC vuông tại A.

a) Xét tam giác ABC vuông tại A có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
⇒ BC = 10 (cm)

∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0

Lê Xuân Trường
1-Xét tam giác ABH và tam giác ACH có
Góc AHB = Góc AHC = 90 độ
AC = AB (Do tam giác ABC cân tại A)
Góc ABH = Góc ACH(Do tam giác ABC cân tại A)
Suy ra tam giác ABH = tam giác ACH (cạnh huyền -góc nhọn )
Suy ra BH = CH =3 cm (2 cạnh tương ứng )
2 . Tui không biết làm thông cảm nhe !

a) Chứng minh được: \(\Delta\)ABE = \(\Delta\)ACD => CD = BE
b ) \(\Delta\)ABE = \(\Delta\)ACD => ^ABE = ^ACD
Gọi H là giao điểm của CD và BE
=> ^HBD = ^ACD
Lại có: ^HDB = ^ADC ( đối đỉnh )
=> ^HBD + ^HDB = ^ACD + ^ADC = 90 độ
=> ^DHB = 180o - ( ^HBD + ^HDB ) = 90 độ
=> CD vuông BE
c) Xét \(\Delta\)EAD có: ^EAD = 90 độ và EA = ED => \(\Delta\)EAD vuông cân => ^EDA = 45 độ
=> ^MDB = ^EDA = 45 độ ( đối đỉnh )
Ta có: BD vuông AC ; CD vuông BE => D là trực tập \(\Delta\)ECB => ED vuông BC => ^DMB = 90 độ
Xét \(\Delta\)DMB có: ^DBM = 180o - ( ^MDB + ^DMB ) = 180 độ - ( 90o + 45o ) = 45o
=> ^MDB = ^DBM => \(\Delta\)DMB cân tại M => MB = MD
Bài 2: Theo cách lớp 7.
H A C B K M
Kẻ BH vuông AC tại H => ^BAH = 180o - ^BAC = 180o - 120o = 60o
=> \(\Delta\)HBA là nửa tam giác đều ( học cái này chưa? )
=> AH = \(\frac{1}{2}\).AB = \(\frac{1}{2}\).4 = 2 ( cm )
Xét \(\Delta\)HAB vuông tại H có: AH = 2 cm ; AB = 4 cm
Dùng định lí Pitago => \(BH^2=AB^2-AH^2=4^2-2^2=12\)=> \(BH=2\sqrt{3}\)(cm)
Xét \(\Delta\)BHC vuông tại H có: \(BH=2\sqrt{3}\)cm ; HC = HA + AC = 2 + 6 = 8 cm
Theo định lí Pitago => \(BC^2=BH^2+HC^2=\left(2\sqrt{3}\right)^2+8^2=76\)=> \(BC=2\sqrt{19}\)( cm )
Vì M là trung điểm BC => \(BM=\sqrt{19}\)cm
Kẻ AK vuông BC tại K
Ta có: \(S\left(ABC\right)=\frac{1}{2}.BH.AC=\frac{1}{2}AK.BC\)( diện tích tam giác ABC )
=> \(BH.AC=AK.BC\)=> \(2\sqrt{3}.6=AK.2\sqrt{19}\Rightarrow AK=\frac{6\sqrt{57}}{19}\)cm
Xét \(\Delta\)BAK vuông tại K có: \(AB=4cm;AK=\frac{6\sqrt{57}}{19}\)cm
Theo định lí Pitago => \(BK^2=AB^2-AK^2\)=> \(BK=\frac{14\sqrt{19}}{19}\)cm
=>KM = BM - BK = \(\sqrt{19}-\frac{14\sqrt{19}}{19}=\frac{5\sqrt{19}}{19}\)cm
Xét \(\Delta\)AKM có: \(KM=\frac{5\sqrt{19}}{19}\)cm và \(AK=\frac{6\sqrt{57}}{19}\)cm
=> \(AM^2=AK^2+KM^2=\left(\frac{5\sqrt{19}}{19}\right)^2+\left(\frac{6\sqrt{57}}{19}\right)^2=7\)
=> \(AM=\sqrt{7}\)
a) Xét tam giác ABC vuông tại A có:
A B 2 + A C 2 = B C 2 ⇒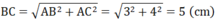
Ta có:
AH.BC = AB.AC ⇒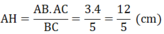
sinB = AC/BC = 4/5 ⇒ ∠B = 53 , 1 0
⇒ ∠C = 90 0 - ∠B = 36 , 9 0