Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ΔABC đồng dạng với ΔMNP
=>\(\dfrac{AB}{MN}=\dfrac{BC}{NP}=\dfrac{AC}{MP}\)
ΔABC đồng dạng với ΔMNP
=>Độ dài cạnh nhỏ nhất của ΔMNP sẽ là độ dài tương ứng với cạnh nhỏ nhất của ΔABC
mà cạnh nhỏ nhất của ΔABC là AB và cạnh tương ứng của AB trong ΔMNP là MN
nên MN=2,5cm
=>\(\dfrac{5}{2,5}=\dfrac{12}{MP}=\dfrac{13}{NP}\)
=>\(\dfrac{12}{MP}=\dfrac{13}{NP}=2\)
=>MP=12/2=6(cm); NP=13/2=6,5(cm)
Áp dụng định lí Pytago cho tam giác vuông ABC, ta có BC=13cm => R=6,5cm
Đáp án là C
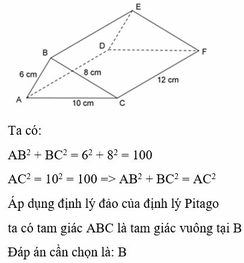
Tam giác ABC có:
A B 2 + A C 2 = 12 2 + 16 2 = 400 = B C 2
⇒ ΔABC vuông tại A
⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của BC
⇒ Bán kính = 10 cm
a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: góc C=180-50-60=70 độ
Xét ΔABC có góc A<góc B<góc C
nên BC<AC<AB
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
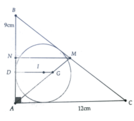
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
a, ΔABC có MN // BC
⇒ ΔAMN ~ ΔABC
⇒ \(\frac{AM}{AB}=\frac{MN}{BC}\)
⇒ MN = \(\frac{3}{12}\). 16
⇒ MN = 4 (cm)
b, ΔABI có MK // BI (MN // BC), theo hệ quả của định lí Ta lét ta có:
\(\frac{MK}{BI}=\frac{AK}{AI}\) (1)
ΔACI có BK // CI (MN // BC), theo hệ quả của định lí Ta lét ta có:
\(\frac{NK}{CI}=\frac{AK}{AI}\) (2)
Từ (1), (2) ⇒ \(\frac{MK}{BI}=\frac{NK}{CI}\)
Mà BI = CI (I là trung điểm của BC)
⇒ MK = NK
⇒ K là trung điểm của MN (đpcm)
c,