Cho tam giác có Â=90o; AB<AC. Trên cạnh AC lấy điểm D sao cho AD=AB. trên tia đối của tia AB lấy điểm E sao cho AE=AC.
a) Biết 4B=5C .Tính góc AED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra; BD=CE
b: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
AE=AD
Do đó: ΔAEH=ΔADH
Suy ra: \(\widehat{EAH}=\widehat{DAH}\)
hay AH là tia phân giác của góc BAC
c: Xét ΔABC cso AE/AB=AD/AC
nên DE//BC

Lấy E∈AD�∈�� sao cho AE=AB��=�� mà AD=AB+AC��=��+�� nên AC=DE.��=��.
ΔABEΔ��� cân có ˆBAD=60∘���^=60∘ nên ΔABEΔ��� là tam giác đều suy ra AE=EB.��=��.
Thấy ˆBED=ˆEBA+ˆEAB=120∘���^=���^+���^=120∘ (góc ngoài tại đỉnh E� của tam giác ABE��� ) nên ˆBED=ˆBAC(=120∘)���^=���^(=120∘)
Suy ra ΔEBD=ΔABC(c.g.c)⇒ˆB1=ˆB2Δ���=ΔA��(�.�.�)⇒�1^=�2^ (hai góc tương ứng bằng nhau) và BD=BC��=�� (hai cạnh tương ứng)
Lại có ˆB1+ˆB3=60∘�1^+�3^=60∘ nên ˆB2+ˆB3=60∘.�2^+�3^=60∘.
ΔBCDΔ��� cân tại B� có ˆCBD=60∘���^=60∘ nên nó là tam giác đều.
Đây nhé!

a) Xét ΔBAD và ΔBED có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔBAD=ΔBED(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)
hay DE⊥BE(Đpcm)
b) Ta có: ΔBAD=ΔBED(Cmt)
nên AD=ED(Hai cạnh tương ứng)
Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(Đpcm)

Tam giác ABC là tam giác vuông nên góc A là góc lớn nhất, suy ra cạnh lớn nhất là BC. Chọn B

Hai tam giác AHC và BAC có:
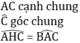
Nhưng hai tam giác này không bằng nhau vì góc AHC không phải là góc kề với cạnh AC

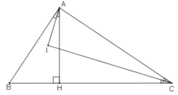
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.