Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
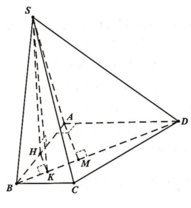
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.

Đáp án D
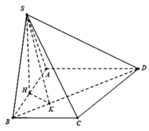
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: ![]()
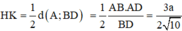
Do đó 
Vậy 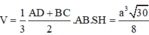

Chọn D
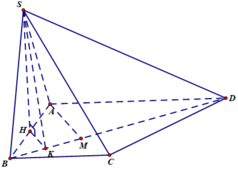
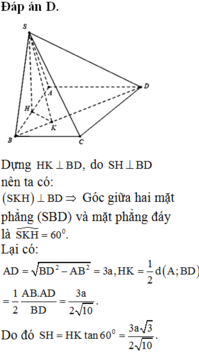
Ta có ![]()
Gọi H là trung điểm AB thì ![]() ,
,
kẻ ![]() , ta có
, ta có ![]() là góc giữa (SBD) và (ABCD), do đó
là góc giữa (SBD) và (ABCD), do đó ![]() = 600
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
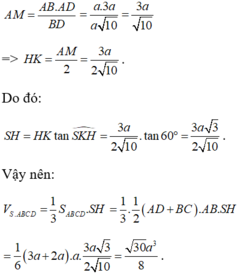

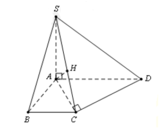
a, Ta có: \(\left\{{}\begin{matrix}AB\perp SA\left(do:SA\perp\left(ABCD\right)\right)\\AB\perp AD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SAD\right)\)
Từ C kẻ CH // AB ⇒ CH ⊥ (SAD)
⇒ d (C, (SAD)) = CH = 2a
b, Ta có: \(\left(SAC\right)\cap\left(ABCD\right)=AC\)
Hạ DE ⊥ AC ⇒ DE ⊥ (SAC)
⇒ d(D, (SAC)) = DE
Ta có: AC = 2a√2, AH = HC 2a và HD = a
Xét tam giác HDC vuông tại H, có: \(DC=\sqrt{HD^2+HC^2}=a\sqrt{5}\)
Xét tam giác AHC vuông cân tại H, có: \(\widehat{HAC}=45^o=\widehat{DAE}\)
Xét tam giác ADE vuông tại E, có: \(DE=AD.sin\widehat{DAE}=\dfrac{3a\sqrt{2}}{2}\)


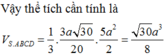

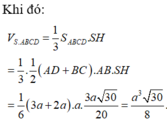

Xét tứ giác ABCE có
là hình bình hành.
Lại có
là hình vuông cạnh a.
Bán kính đường tròn ngoại tiếp hình vuông ABCE là
R d = a 2 2
Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
S.ABCE là:
Chọn B.