Cho tam giác $ABC$ vuông tại $A$ có các cạnh $A B=9 cm ; A C=12 cm$
a) Tính độ dài $BC$
b) Kẻ đường cao $AH$. Tính độ dài đoạn thẳng $AH$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15cm
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20cm
Vậy: AB=15cm; AC=20cm
Ta có: BH+CH=BC(H nằm giữa B và C)
hay BC=9+16=25cm
Ta có: \(AB^2+AC^2=15^2+20^2=625\)
\(BC^2=25^2=625\)
Do đó: \(BC^2=AB^2+AC^2\)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)

dùng Pitago đảo thử từng cặp 1 thôi:v
ta có: \(\left(b-c\right)^2+h^2=b^2+c^2-2bc+h^2\)(1)
vì tam giác ABC vuông ở A có đường cao AH nên \(a^2=b^2+c^2\)và\(AB.AB=AH.BC=2S\)hay\(b.c=a.h\)
\(\Rightarrow b^2+c^2-2bc+h^2=a^2-2ah+h^2=\left(a-h\right)^2\)

bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

a. Xét tam giác vuông ABC
Theo định lý Py - ta - go ta có :
AB2 + AC2 = BC2
=> 32 + AC2 = 52
=> 9 + AC2 = 25
=> AC2 = 16
=> AC = 4
Vậy AB < AC < BC
b. Xét tam giác BAM và tam giác BDM ta có :
BM chung
Góc BAM = góc BDM ( = 90 độ )
BA = BD ( gt)
=> tam giác BAM = tam giác BDM ( ch - cgv)
=> MA = MD ( hai cạnh tương ứng )
Xét tam giác AMN và tam giác DMC
góc AMN = góc DMC ( đối đỉnh )
MA = MD ( cmt)
góc MAN= góc MDC ( = 90 độ )
=> Tam giác AMN = tam giác DMC
=> MN = MC
=> Tam giác MNC cân
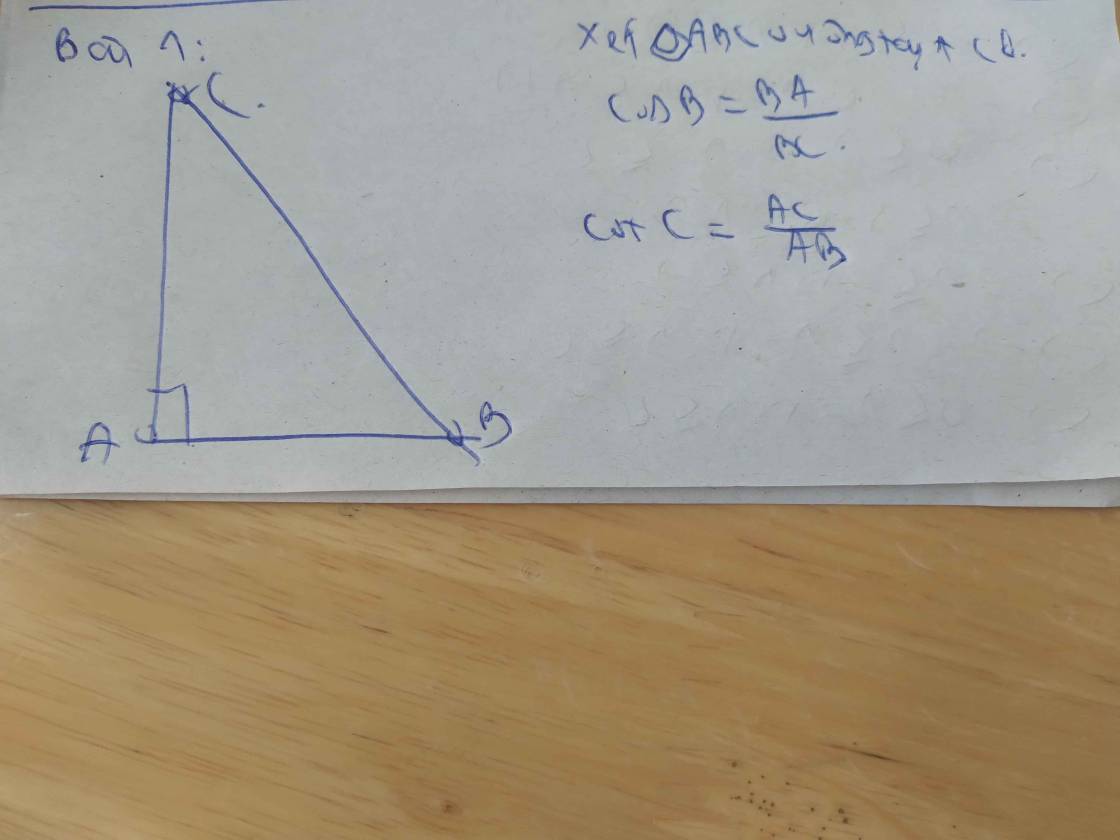

a, Theo định lí Pytag tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=15cm\)
b, Áp dụng hệ thức \(BC.AH=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{36}{5}cm\)