cho hệ phương trình: 2mx+y=2 ; 8x +my=m+2
tìm m để 4x+3y=7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 12 2019
Thay m = 2 vào hệ ta được x + y = 2 2 x + y = 3
Khi đó x + y = 2 2 x + y = 3 ⇔ x + y = 2 x = 1 ⇔ x = 1 y = 1
Vậy hệ phương trình có nghiệm duy nhất (1; 1) khi m = 2
Đáp án: D
CM
26 tháng 4 2019
Đáp án D
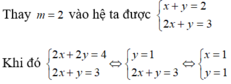
Vậy hệ phương trình có nghiệm duy nhất (1; 1) khi m = 2
T
18 tháng 1 2021
Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
9 tháng 1 2023
2mx+y=2 và 8x+my=m+2
=>y=2-2mx và 8x+m(2-2mx)=m+2
=>\(\left\{{}\begin{matrix}8x+2m-2m^2x-m-2=0\\y=-2mx+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(-2m^2+8\right)=-m+2\\y=-2mx+2\end{matrix}\right.\)
=>2(m-2)(m+2)x=m-2 và y=-2mx+2
Nếu m=2 thì hệpt có vô số nghiệm
Nếu m=-2 thìhệ pt vn
Nếu m<>2; m<>-2 thì hệ phương trình có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{1}{2\left(m+2\right)}\\y=-2m\cdot\dfrac{1}{2\left(m+2\right)}+2=-\dfrac{m}{m+2}+2=\dfrac{-m+2m+4}{m+2}=\dfrac{m+4}{m+2}\end{matrix}\right.\)
CM
10 tháng 8 2018
Để hệ phương trình − m x + y = − 2 m x + m 2 y = 9 nhận cặp (1; 2) làm nghiệm thì − m .1 + 2 = − 2 m 1 + m 2 2 = 9 ⇔ m = − 2 m = ± 2 ⇒ m = − 2
Vậy m = −2
Đáp án: C
KC
3
9 tháng 12 2016
Mình giải bằng định thức Grane nhé :
\(D=-6m-m=-7m\)
\(D_x=15-1=14\)
\(D_y=-2m-5m=-7m\)
Để hệ phương trình có nghiệm thì \(\orbr{\begin{cases}D\ne0\\D=D_x=D_y=0\end{cases}}\)
TH1. \(D\ne0\Rightarrow m\ne0\) , hệ phương trình có nghiệm \(\hept{\begin{cases}x=\frac{D_x}{D}=\frac{14}{-7m}=-2m\\y=\frac{D_y}{D}=\frac{-7m}{-7m}=1\end{cases}}\)
TH2. \(D=D_x=D_y=0\)
Ta nhận thấy ngay \(D_x=14\ne0\), do vậy trường hợp này không xảy ra.
Vậy để hệ phương trình có nghiệm thì \(m\ne0\)
16 tháng 12 2023
a: Khi m=-1 thì hệ phương trình sẽ là:
\(\left\{{}\begin{matrix}x\cdot2\cdot\left(-1\right)-3y=2\cdot\left(-1\right)-1\\4x-\left(-1+5\right)y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x-3y=-3\\4x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-4x-6y=-6\\4x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6y-4y=-6+2\\x-y=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-10y=-4\\x-y=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{5}\\x=\dfrac{1}{2}+\dfrac{2}{5}=\dfrac{9}{10}\end{matrix}\right.\)
b: Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{2m}{4}\ne-\dfrac{3}{-\left(m+5\right)}\)
=>\(\dfrac{m}{2}\ne\dfrac{3}{m+5}\)
=>\(m^2+5m\ne6\)
=>\(m^2+5m-6\ne0\)
=>\(\left(m+6\right)\left(m-1\right)\ne0\)
=>\(m\notin\left\{-6;1\right\}\)
c: \(\left\{{}\begin{matrix}2mx-3y=2m-1\\4x-\left(m+5\right)y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4mx-6y=4m-2\\4mx-\left(m^2+5m\right)y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-6y+\left(m^2+5m\right)y=2m-2\\4x-\left(m+5\right)y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(m^2+5m-6\right)=2m-2\\4x-\left(m+5\right)y=2\end{matrix}\right.\)(1)
Khi \(m\notin\left\{-6;1\right\}\) thì hệ phương trình (1) sẽ trở thành:
\(\left\{{}\begin{matrix}y=\dfrac{2m-2}{m^2+5m-6}=\dfrac{2\left(m-1\right)}{\left(m+6\right)\left(m-1\right)}=\dfrac{2}{m+6}\\4x=2+\left(m+5\right)y=2+\dfrac{2m+10}{m+6}=\dfrac{4m+22}{m+6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{2}{m+6}\\x=\dfrac{4m+22}{4m+24}=\dfrac{2m+11}{2m+12}\end{matrix}\right.\)
Để hệ có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(\left\{{}\begin{matrix}m\notin\left\{-6;1\right\}\\\dfrac{2}{m+6}>0\\\dfrac{2m+11}{2m+12}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\notin\left\{-6;1\right\}\\m+6>0\\\dfrac{2m+11}{m+6}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m>-6\\\left[{}\begin{matrix}\left\{{}\begin{matrix}2m+11>0\\m+6>0\end{matrix}\right.\\\left\{{}\begin{matrix}2m+11< 0\\m+6< 0\end{matrix}\right.\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m>-6\\\left[{}\begin{matrix}m>-\dfrac{11}{2}\\m< -6\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}m\ne1\\m>-\dfrac{11}{2}\end{matrix}\right.\)
Để hệ có nghiệm duy nhất thì \(\dfrac{2m}{8}\ne\dfrac{1}{m}\)
=>\(m^2\ne4\)
=>\(m\notin\left\{2;-2\right\}\)
\(\left\{{}\begin{matrix}2mx+y=2\\8x+my=m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m^2\cdot x+my=2m\\8x+my=m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(2m^2-8\right)=m-2\\y=2-2mx\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{m-2}{2m^2-8}=\dfrac{1}{2\left(m+2\right)}\\y=2-\dfrac{2m}{2\left(m+2\right)}=2-\dfrac{m}{m+2}=\dfrac{2m+4-m}{m+2}=\dfrac{m+4}{m+2}\end{matrix}\right.\)
4x+3y=7
=>\(\dfrac{4}{2\left(m+2\right)}+\dfrac{3\left(m+4\right)}{m+2}=7\)
=>\(\dfrac{2+3\left(m+4\right)}{m+2}=7\)
=>7(m+2)=2+3m+12
=>7m+14=3m+14
=>4m=0
=>m=0(nhận)