Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau: Có tâm I(5; -3; 7) và có bán kính r = 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(x-5\right)^2+\left(y+3\right)^2+\left(z-7\right)^2=4\)
b) \(\left(x-4\right)^2+\left(y+4\right)^2+\left(z-2\right)^2=36\)
c) \(\left(x-3\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=18\)

Đáp án B
Đường thẳng d đi qua điểm M(6 ;1 ;0) và có vectơ chỉ phương là u d → = (4; -1; -1). Ta có:
![]()
Do đường thẳng d tiếp xúc với mặt cầu (S) nên (S) có bán kính là:
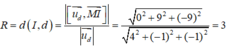
Vậy phương trình của mặt cầu (S) là : ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 9

Đáp án A
Phương pháp giải:
Khoảng cách từ tâm đến trục Oz chính bằng bán kính R
Phương trình mặt cầu tâm và bán kính
![]()
Lời giải:
Phương trình trục Oz
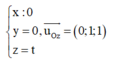
Ta có
![]()
Khoảng cách từ tâm I -> Oz là
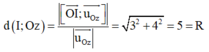
Vì (S) tiếp xúc với trục Oz Þ Phương trình cần tìm là ( S ) : x - 3 2 + y - 4 2 + z + 2 2 = 25

Đáp án A
Xét mặt cầu S : x − 1 2 + y + 3 2 + z 2 = 5 có tâm I 1 ; − 3 ; 0 và bán kính R = 5

Đáp án C
Đường thẳng d đi qua điểm M(-2 ;3 ;2) và có vectơ chỉ phương là u d → = (-4; 1; 1). Ta có:

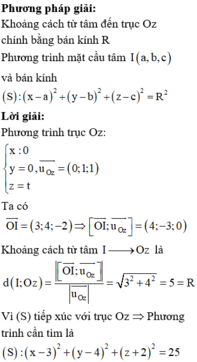
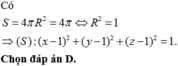
x - 5 2 + y + 3 2 + z - 7 2 = 4