Lập phương trình thanh số, phương trình tổng quát của đường thẳng Δ biết: d. Δ đi qua D(2; 5) và E(3; 1)
e. Δ đi qua G(2; 5) và song song với đường thẳng d: 2x-3y-3 = 0
g. Δ đi qua H(2; 5) và vuông góc với đường thẳng d: x + 3y + 2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
25 tháng 4 2023
Đúng(0)
Những câu hỏi liên quan
11 tháng 5 2023
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
CM
5 tháng 6 2018
a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒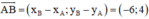 
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận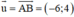 
là một vtcp
⇒ Δ nhận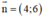 
là một vtpt.
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.
CM
8 tháng 8 2018
Chọn D.
Phương trình tổng quát của đường thẳng Δ đi qua điểm M(-1;2) và có hệ số góc k = 3 là: y = 3(x + 1) + 2 ⇔ 3x - y + 5 = 0
AH
Akai Haruma
Giáo viên
27 tháng 2 2021
Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
27 tháng 2 2021
Tại sao từ cos 450=\(\dfrac{\sqrt{2}}{2}\) thì lại => a=3b hoặc a=\(\dfrac{-b}{3}\) ạ ?
CM
8 tháng 5 2019
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
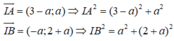
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
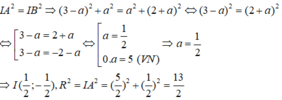
Vậy phương trình đường tròn có dạng:
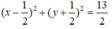
Ta có:
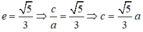
Giả sử elip (E) có dạng:
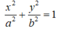
Vì (E) đi qua B nên:
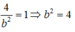
Mà
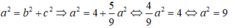
Vậy phương trình chính tắc của elip (E) là:
9 tháng 3 2022
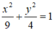
bạn xem lại lớp nhé
(d) // đt (delta) <=> \(\left\{{}\begin{matrix}a=5\\b\ne1\end{matrix}\right.\)
=> (d) : y = 5x + b
(d) đi qua M(-1;2) <=> 2 = -5 + b <=> b = 7 (tm)
Vậy (d) : y = 5x + 7
AH
Akai Haruma
Giáo viên
28 tháng 2 2023
Lời giải:
a
VTPT: $(-2,5)$
PTĐT $(\Delta)$ là; $-2(x-1)+5(y-3)=0$
$\Leftrightarrow -2x+5y-13=0$
b. PTĐT $(\Delta)$ là:
$1(x-2)+4(y-1)=0\Leftrightarrow x+4y-6=0$
c.
VTCP của $(\Delta)$ là: $\overrightarrow{AB}=(2,5)$
$\Rightarrow$ VTPT của $(\Delta)$ là: $(-5,2)$
PTĐT $(\Delta)$ là: $-5(x-1)+2(y+2)=0$
$\Leftrightarrow -5x+2y+9=0$
d.
Làm tương tự câu c, PT $3x+2y-6=0$
MS
27 tháng 4 2022
a) Ta có: \(\overrightarrow{\text{BC}}\) = (1; -7)
\(\overrightarrow{\text{ }n_{\text{BC}}}\)= (7; 1)
PTTQ: 7(x - 5) + 1(y - 5) = 0
=> 7x - 35 + y - 5 = 0
=> 7x + y - 40 = 0
b) Ta có: \(\overrightarrow{\text{AC}}\) = (8; -6)
=> \(\text{AC}=\sqrt{8^2+6^2}=10\)
Phương trình đường tròn là:
(x + 2)2 + (y - 4)2 = 100
c) (C): (x + 2)2 + (y - 4)2 = 100
Ta có: \(\text{AM}=\sqrt{2^2+5^2}=\sqrt{29}\)
Để HK ngắn nhất => d(A; Δ) lớn nhất
=> d(A; Δ) = AM => AM ⊥ Δ
=> \(\overrightarrow{\text{n}_{\Delta}}\) = \(\overrightarrow{\text{AM}}\)
=> \(\overrightarrow{\text{n}_{\Delta}}\) = (-2; -5)
=> \(\text{2}\left(x+4\right)+5\left(y+1\right)=0\)
=> \(\text{ }2x+5y+13=0\)