Cho hàm số y = x 3 − 3 m x 2 + 6 , giá trị nhỏ nhất của hàm số trên 0 ; 3 bằng 2
A. m = 2
B. m = 31 27
C. m > 3 2
D. m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3

Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
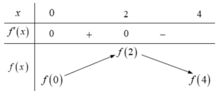
Từ bảng biến thiên ta có ![]()
Mặt khác ![]()
![]()
![]()
![]()
Suy ra ![]()

Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
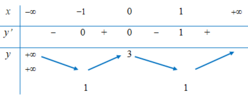
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
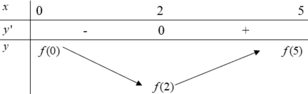
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
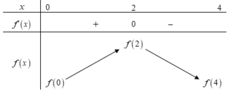
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Đáp án D
Tính y’ và tìm nghiệm của y ' = 0 .
- Biện luận các trường hợp điểm x=3 nằm trong, nằm ngoài khoảng 2 nghiệm để suy ra kết luận.
Cách giải:
TXĐ: D = R
y ' = 3 x 2 − 6 m x
Ta có: y ' = 0 ⇔ x = 0 → y = 6 x = 2 m → y = − 4 m 3 + 6
Xét TH1: m=0 . Hàm số đồng biến trên 0 ; 3 . ⇒ M i n 0 ; 3 y = y 0 = 6 → loại.
Xét TH2: m ≥ 3 2 ⇒ 2 m > 3 > 0 . Khi đó, hàm số nghịch biến trên 0 ; 3 ⊂ 0 ; 2 m
⇒ M i n 0 ; 3 y = y 3 = 33 − 27 m = 2 → m = 31 27 < 3 2 (loại)
Xét TH3: 3 2 > m > 0 ⇒ 3 > 2 m > 0 thì đồ thị hàm số có điểm cực đại là 0 ; 6 và điểm cực tiểu là 2 m , − 4 m 3 + 6 .
Khi đó , GTNN trên 0 ; 3 là y 2 m = − 4 m 3 + 6
⇒ − 4 m 3 + 6 = 2 ⇔ m 3 = 1 ⇔ m = 1 (thỏa mãn)
Xét TH4: m < 0 → 0 ; 6 là điểm cực tiểu và trên 0 ; 3 hàm số đồng biến.
⇒ y min = 6 → loại.
Vậy m=1 là giá trị cần tìm.
Đáp án D.
Chú ý khi giải:
HS cần phải xét tất cả các trường hợp và chú ý loại nghiệm. nhiều em sai lầm kết luận m = 31 27 mà không chú ý điều kiện của trường hợp đó là m ≥ 3 2