Chứng minh: (2m - 1; 2n - 1) = 2(m; n) - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CA
0
5 tháng 8 2023
\(m\left(2m-3\right)-2m\left(m+1\right)\)
\(=2m^2-3m-2m^2-2m=-5m⋮5\Rightarrow dpcm\)
KV
5 tháng 8 2023
\(m\left(2m-3\right)-2m\left(m+1\right)\)
\(=2m^2-3m-2m^2-2m\)
\(=-5m⋮5\) \(\forall m\in Z\)
Vậy \(m\left(2m-3\right)-2m\left(m+1\right)⋮m\left(\forall m\in Z\right)\)
22 tháng 5 2016
ta có: 2m4 có mũ =4 suy ra 2m4 có m là âm hay dương thì 2m4 đều thuộc N*.
2m<2m4 ( khi m khác 0) đặt đây là TH1
và 2m=2m4 (khi m = 0) đặt đây là TH2
TH1: 2m<2m4 (m khác 0)
suy ra 2m4+2m là dương
suy ra 2m4+2m+1 là dương > 0 (ĐPCM)
TH2: 2m=2m4 (m=0)
suy ra 2m4+2m=0=0
suy ra 2m4+2m+1=0+1=1>0 (ĐPCM)
Vậy 2m4+2m+1 >0
MN
1
1 tháng 1 2019
Đặt A= (2m-1)3 -(2m-1) =(2m-1)[ (2m-1)2 -1] = (2m-1)(2m-1-1)(2m-1+1)
= (2m-1)(2m-2)(2m) = 4m(2m-1)(m-1)
Nếu m = 2k (k\(\in\) Z) => A= 4.2k.(4k-1)(2k-1) = 8k(4k-1)(2k-1) ⋮ 8
Nếu m=2k+1 (k\(\in\) Z) => A= 4.(2k+1).(4k).(2k) = 32k2 .(2k+1) ⋮ 8
Vậy với \(\forall\) m thì (2m-1)3- (2m-1)⋮ 8
CM
19 tháng 2 2019
Gọi ƯCLN (2m;2m+1)=d
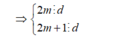
(2m+1) -2m ⋮ d → 1 ⋮ d → d=1
ƯCLN(2m,2m+1) =1
Vậy 2m và 2m+1 là số nguyên tố cùng nhau
A
12 tháng 11 2015
GỌi d là ƯC(2m+1,2m)
=>2m chia hết cho d
=>2m+1 chia hết cho d
=> (2m+1)-(2m) chia hết cho d
=>1 chia hết cho d
=> d =1
vậy 2m và 2m+1 là 2 số nguyên tố cùng nhau
NA
1
AH
Akai Haruma
Giáo viên
29 tháng 1 2020
Lời giải:
Vì $m,m+1$ là 2 số nguyên liên tiếp nên chắc chắn tồn tại một số chẵn, một số lẻ. Do đó $m(m+1)\vdots 2\Rightarrow m(m+1)(2m+1)\vdots 2(1)$
Mặt khác:
Nếu $m\vdots 3\Rightarrow m(m+1)(2m+1)\vdots 3$
Nếu $m$ chia $3$ dư $1\Rightarrow 2m+1\vdots 3\Rightarrow m(m+1)(2m+1)\vdots 3$
Nếu $m$ chia $3$ dư $2\Rightarrow m+1\vdots 3\Rightarrow m(m+1)(2m+1)\vdots 3$
Tóm lại $m(m+1)(2m+1)\vdots 3$ với mọi $m$ nguyên $(2)$
Từ $(1);(2)\Rightarrow m(m+1)(2m+1)\vdots (2.3=6)$
QN
1
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
Lời giải:
Gọi $d$ là ƯCLN của $m$ và $n$. Khi đó:
$m=dx; n=dy$ với $x,y$ là 2 số nguyên dương nguyên tố cùng nhau.
\(2^m-1=2^{dx}-1=(2^d)^x-1\vdots 2^d-1\)
\(2^n-1=2^{dy}-1=(2^d)^y-1\vdots 2^d-1\)
Vì $(2^m-1, 2^n-1)=1$ nên $2^d-1=1$
$\Rightarrow d=1$
Tức là $(m,n)=1$