Có bao nhiêu giá trị nguyên của tham số m trên đoạn
[-2020; 2020] để hàm số f(x) = \(\dfrac{\sqrt{x^2-2x+3}}{x^2-2x+m-1}\) có tập xác định là R?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 4 2017
Chọn B
Tập xác định D = ℝ \{1}
Ta có 
Do đó hàm số nghịch biến trên đoạn [2;3]
Suy ra 
Vậy có 1 giá trị nguyên dương của m.
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 11 2021
ĐKXĐ: \(x\ge0\)
\(x^2+1+\left(2-m\right)x-2\sqrt{x\left(x^2+1\right)}=0\)
Với \(x=0\) ko phải nghiệm, với \(x>0\) chia 2 vế cho x:
\(\Rightarrow\dfrac{x^2+1}{x}+2-m-2\sqrt{\dfrac{x^2+1}{x}}=0\)
Đặt \(\sqrt{\dfrac{x^2+1}{x}}=t\ge\sqrt{2}\)
\(\Rightarrow t^2-2t+2=m\)
Xét hàm \(f\left(t\right)=t^2-2t+m\) khi \(t\ge\sqrt{2}\)
\(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=1< \sqrt{2}\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt{2}\)
\(\Rightarrow f\left(t\right)\ge f\left(\sqrt{2}\right)=4-2\sqrt{2}\)
\(\Rightarrow\) Pt có nghiệm khi \(m\ge4-2\sqrt{2}\)
CM
19 tháng 6 2018
Hàm số y = ln x 2 - 2 x - m + 1 xác định trên R
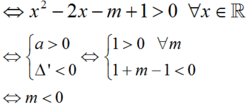
Mà
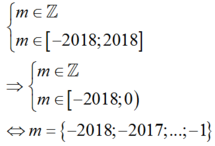
Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A.
CM
14 tháng 2 2017
Chọn D
Phương pháp:
Sử dụng: Hàm số y = ax+b đồng biến ⇔ a > 0, từ đó kết hợp điều kiện đề bài để tìm các giá trị của m.
Cách giải:
Hàm số y = (m-2)x + 2 đồng biến trên ℝ ⇔ m - 2 > 0 ⇔ m > 2
Mà 
=> có 2016 giá trị nguyên của m thỏa mãn đề bài.
CM
30 tháng 9 2019
Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.
