Tính tổng S các nghiệm của phương trình (2 cos2 x+5) ( s i n 4 x - c o s 4 x ) +3=0 trong khoảng ( 0 ; 2 π )
A. S=11 π /6
B. S=4 π
C. S=5 π
D. S=7 π /6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

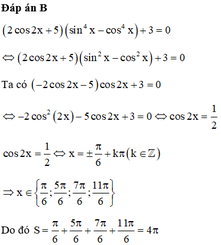

Chọn D.
Đặt t = 2x + 2-x, suy ra t2 = 22x + 2 -2x + 2.
Ta có ![]()
Phương trình trở thành
![]()
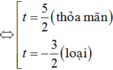
![]()
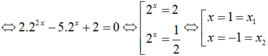
khi đó ; S = x1+ x2 = 0.

\(\left(2cos2x+5\right)\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)+3=0\)
\(\Leftrightarrow-cos2x\left(2cos2x+5\right)+3=0\)
Đặt \(cos2x=a\) (\(-1\le a< 1\))
\(\Leftrightarrow2a^2+5a-3=0\) \(\Rightarrow\left[{}\begin{matrix}a=\frac{1}{2}\\a=-3< -1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow cos2x=\frac{1}{2}\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{3}+k2\pi\\2x=-\frac{\pi}{3}+l2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k\pi\\x=-\frac{\pi}{6}+l\pi\end{matrix}\right.\)
Do \(x\in\left(0;2\pi\right)\Rightarrow x=\left\{\frac{\pi}{6};\frac{5\pi}{6};\frac{11\pi}{6}\right\}\) \(\Rightarrow\sum x=\frac{17\pi}{6}\)

a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 