Cho hàm số y=f(a)=3x\(^2\)
a)Tính giá trị của hàm số lần tại -3; 2\(\sqrt{2}\)và 1-2\(\sqrt{3}\)
b) Tìm a biết f(a)=12+6\(\sqrt{3}\)
c) Tìm b biết f(b)\(\ge\)6b+12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(f\left( 1 \right) = 3.1 = 3;f\left( { - 2} \right) = 3.\left( { - 2} \right) = - 6;f\left( {\dfrac{1}{3}} \right) = 3.\dfrac{1}{3} = 1\).
b) Ta có: \(f\left( { - 3} \right) = 3.\left( { - 3} \right) = - 9;f\left( { - 1} \right) = 3.\left( { - 1} \right) = - 3\)
\(f\left( 0 \right) = 3.0 = 0;f\left( 2 \right) = 3.2 = 6;f\left( 3 \right) = 3.3 = 9\);
Ta lập được bảng sau
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(y\) | –9 | -6 | –3 | 0 | 3 | 6 | 9 |

a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d; 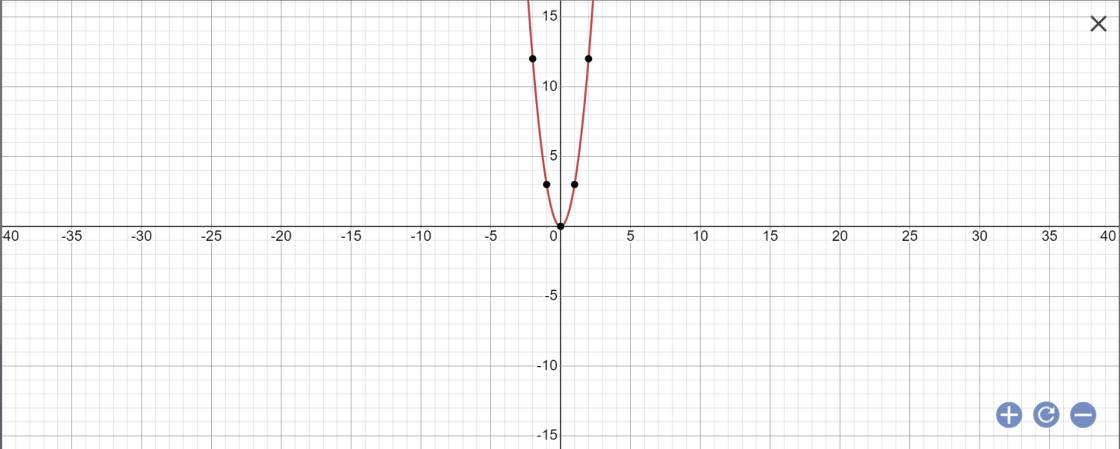

1.
y=f(-1)=3*(-1)-2=-5
y=f(0)=3*0-2=-2
y=f(-2)=3*(-2)-2=-8
y=f(3)=3*3-2=7
Câu 2,3a làm tương tự,chỉ việc thay f(x) thôi.
3b
Khi y=5 =>5=5-2*x=>2*x=0=> x=0
Khi y=3=>3=5-2*x=>2*x=2=>x=1
Khi y=-1=>-1=5-2*x=>2*x=6=>x=3
f(-1)=3.1-2=3-2=1
f(0)=3.0-2=0-2=-2
f(-2)=3.(-2)-2=-6-2=-8
f(3)=3.3-2=9-2=7

\(y=-4\\ \Rightarrow-4=3x^2-7\\ \Rightarrow3x^2=3\\ \Rightarrow x^2=1\\ \Rightarrow x=\pm1\)
\(y=5\\ \Rightarrow5=3x^2-7\\ \Rightarrow3x^2=12\\ \Rightarrow x^2=4\\ \Rightarrow x=\pm2\)
\(y=-6\dfrac{2}{3}\\ \Rightarrow-6\dfrac{2}{3}=3x^2-7\\ \Rightarrow3x^2=\dfrac{1}{3}\\ \Rightarrow x^2=\dfrac{1}{9}\\ \Rightarrow x=\pm\dfrac{1}{3}\)

a, Ta có : \(\left|x-1\right|=2x+1\)
\(\orbr{\begin{cases}x-1=2x+1\\x-1=-2x-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}-x=2\\3x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=0\end{cases}}}\)
* Trường hợp 1 : \(y=3x-1\Leftrightarrow y=6-1=5\)
* Trường hợp 2 : \(y=2x+1\Leftrightarrow y=0+1=1\)
b, Theo bài ra ta có : \(f\left(3x-1\right)=-1\)hay
\(3.\left(-1\right)-1=-3-1=-4\)

Đáp án C.
Hàm số liên tục nếu:
lim x → − 2 + f x = lim x → − 2 − f x = f 2 ⇔ 3. − 2 − 5 = − 2 a − 1 ⇔ a = 5.
a: \(f\left(-3\right)=3\cdot9=27\)
\(f\left(2\sqrt{2}\right)=3\cdot8=24\)
\(f\left(1-2\sqrt{3}\right)=3\cdot\left(13-4\sqrt{3}\right)=39-12\sqrt{3}\)
b: Ta có: \(f\left(a\right)=12+6\sqrt{3}=\left(3+\sqrt{3}\right)^2=3\left(\sqrt{3}+1\right)^2\)
nên \(3x^2=3\left(\sqrt{3}+1\right)^2\)
hay \(x\in\left\{\sqrt{3}+1;-\sqrt{3}-1\right\}\)
c.
$f(b)\geq 6b+12$
$\Leftrightarrow 3b^2\geq 6b+12$
$\Leftrightarrow b^2\geq 2b+4$
$\Leftrightarrow b^2-2b-4\geq 0$
$\Leftrightarrow (b-1-\sqrt{5})(b-1+\sqrt{5})\geq 0$
$\Leftrightarrow b\geq 1+\sqrt{5}$ hoặc $b\leq 1-\sqrt{5}$