Trong không gian Oxyz, cho điểm M (1; 1; 2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi n → = ( 1 ; a ; b ) là một véc tơ pháp tuyến của (P). Tính S = a3 - 2b
A. S = 0
B. S = - 3
C. S = 6
D. S = -15/8



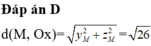
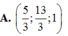
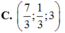
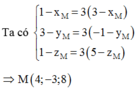
Chọn A
Mặt phẳng (P) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C nên A (a; 0; 0), B (0; b; 0), C (0; 0 ; c) (a, b, c > 0). Phương trình mặt phẳng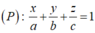
Thể tích khối tứ diện OABC nhỏ nhất khi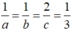 suy ra a = 3, b = 3, c = 6.
suy ra a = 3, b = 3, c = 6.