Cho điểm A(-1

PT

Pham Trong Bach

10 tháng 8 2017

Cho điểm A(-1; 2) và đường thẳng ∆ : x = t - 2 y = - t - 3 .Tìm điểm M sao cho AM ngắn nhất.

A. (-3; -2)

B. (4; -5)

C. (2; -3)

D. Đáp án khác

#Toán lớp 10

1

CM

Cao Minh Tâm

10 tháng 8 2017

Đáp án A

Điểm M( t-2; -t- 3) thuộc ∆.

Có MA²= (t-1) ²+ (-t-3) ²= 2t²+ +4t +10= 2( t²+ 2t +5)=2(t+1)²+ 8 ≥ 8 với mọi t.

Do đó MA² M A 2 ≥ 8 8 suy ra M A ≥ 2 2

Vậy m i n ( M A ) = 3 2 khi t= -1 . Khi đó M( -3; -2)

Đúng(0)

K

༺кëฑ༻

10 tháng 4 2019 - olm

trên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên...

Đọc tiếp

trên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳngtrên tia Ax lấy các điểm B và C sao cho AB=3 AC=6 a) chứng minh rằng B là trung điểm của AC b) lấy 1 điểm D ko thuộc vào đường thẳng làm đc cho 100 t.i.c.k

#Toán lớp 12

0

QT

Quoc Tran Anh Le

Giáo viên

28 tháng 9 2023

Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2).

a) Chứng minh ba điểm A, B, G không thẳng hàng.

b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC.

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

28 tháng 9 2023

a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)

Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng

b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)

Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)

Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)

Đúng(0)

DV

Đặng vân anh

7 tháng 6 2015 - olm

1) Cho điểm B nằm giữa 2 điểm A và D,điểm D nằm giữa hai điểm A và E, điểm E nằm giữa hai điểm A và C.Hỏi năm điểm A,B,C,D,E có cùng thuộc 1 đường thẳng không,giải thích?

2)Cho điểm O nằm trên đường thẳng xy.Lấy điểm A thuộc tia Ox,điểm B thuộc tia Oy sao cho OA=3cm,OB=5cm.

a)Tính AB

b)Lấy điểm M trên đường thẳng xy có OM =1cm.TínhMB=?

#Toán lớp 6

1

TT

tran thanh minh

7 tháng 6 2015

2 Vì O nằm trên đường thẳng xy suy ra tia Ox đối với tia Oy(*)

mà A thuộc tia Ox

B thuộc tia Oy

mà từ (*) ta có tia OA đối với tia OB suy ra điểm O nằm giữa A,B(**)

từ(**) ta có OA+OB=AB(công thức cộng đoạn thẳng )

3cm+5cm=AB

suy ra AB=8cm

b,TH1 M nằm trên tia OA

vì tia OA là tia đối của tia OB

suy ra tia OM là tia đói của tia OB

suy ra điểm O nằm giữa diểm M,B

suy ra ta có

OM+OB=MB(công thức cộng đoạn thẳng)

1cm+5cm=MB

suy ra MB=6cm

TH2 điểm M nằm trên tia Oy

vì trên tia Oy có điểm M,B(1)

mà OM<OB vì (1cm<5cm)(2)

suy ra diểm M nằm giữa điểm O,B(***)

từ (***) suy ra OM+MB=OB(công thức cộng góc)

1cm+MB=5cm

MB=5cm-1cm

MB=4cm

còn câu a tớ ko biết

Đúng(0)

NC

Nguyễn Chí Tài

15 tháng 12 2015 - olm

Câu 1

Đoạn thẳng AB là hình gồm

A/ Hai điểm A và B

B/ Tất cả các điểm nằm giữa A và B

C/ Tất cả các điểm nằm giữa A và B và cả A,B

Câu2

Có 1 và chỉ 1 đường thẳng đi qua

a) hai điểm cho trước

b) điểm A cho trước

c) hai điểm phân biệt cho trước

#Toán lớp 6

1

NN

Nghĩa Nguyễn

15 tháng 12 2015

câu 1- C

câu 2 - B

Đúng(0)

NM

Ngô Mỹ Tâm

18 tháng 12 2015 - olm

Cho mình hỏi:1)Trên tia Ox lấy hai điểm A và B sao cho OA=1 cm,OB=5 cm.a)Tính CO dài đoạn thẳng ABb)Trên tia đối của tia Ox lấy điểm C sao cho OC=3 cm.Hỏi A có là trung điểm của đoạn thẳng BC ko?Vì sao?2)Trên tia Ox,vẽ hai điểm A và B sao cho OA=1 vm,OB=3 cm.Trên tia đối tia Ox vẽ điểm C sao cho OC=1 cm.a)Tính độ dài đoạn thẳng AB,ACb)Điểm nào là trung điểm của đoạn thẳng nào?Vì...

Đọc tiếp

#Toán lớp 6

0

DK

Đỗ Khánh Ngọc

20 tháng 8 2020 - olm

Cho MN = 6cm .Trên đoạn thẳng MN ,vẽ A sao cho MA =1/3 MN ,vẽ B sao cho NB = 1/3 MN .

a) Điểm A có nằm giữa hai điểm M và N không ? Vi sao ?

b) Chứng tỏ rằng điểm B nằm giữa hai điểm M,N

c) Trong ba điểm A,B,C,D điểm nào nằm giữa hai điểm còn lại ?

#Toán lớp 6

0

NH

nguyễn hoàng lê thi

27 tháng 9 2019

1. Trong mặt phẳng toạ độ Oxy , cho bà điểm A (6;3) , B (-3,6) , C(1;-2). Xác định điểm D trên trục hoành sao cho bà điểm A,B,D thẳng hàng.

2. Cho 4 điểm A(1;-2) , B(0;3) , C(-3,4), D(-1;8). Bà điểm nào trong 4 điểm đã cho là thẳng hàng?

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

27 tháng 9 2019

a/ Gọi \(D\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AD}=\left(a-6;-3\right)\end{matrix}\right.\)

Do A; B; D thẳng hàng \(\Leftrightarrow\frac{a-6}{-9}=\frac{-3}{3}\Rightarrow a=15\) \(\Rightarrow D\left(15;0\right)\)

b/ \(\overrightarrow{AB}=\left(-1;5\right);\) \(\overrightarrow{AD}=\left(-2;10\right)\)

\(\Rightarrow\overrightarrow{AD}=2\overrightarrow{AB}\Rightarrow A,B,D\) thẳng hàng

Đúng(0)

AD

Anh Dao

12 tháng 11 2021

Cho đường thẳng (d) : y = - 2x + 1

a. Điểm nào sau đây thuộc (d):: M(– 1; 3) ; N(1 ; 1) ; K(- 1 /2 ; 0)

b. Tìm toạ độ điểm E thuộc (d)biết Xe = – 2

c.Tìm toạ độ điểm F thuộc(d) biết Yf = 3

d. Cho điểm A( m – 1; 2) thuộc (d) . Tính m ?

#Toán lớp 9

2

AD

Anh Dao

12 tháng 11 2021

giúp mình với mình đang cần gấp

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

12 tháng 11 2021

b: Thay x=-2 vào (d), ta được:

y=4+1=5

Đúng(1)

TC

TRẦN CÔNG THỊNH PHÚ

13 tháng 3 2022

4/ Cho đường thẳng XY,trên XY lấy 1 điểm O.Trên OX lấy 1 điểm A,trên oy lấy 1 điểm B sao cho OA=5cm;AB=10cm. a)Trong 3 điểm A,O,B điểm nào nằm giữa 2 điểm còn lại ? Vì sao ?b)Tính OBc)Điểm O có là trung điểm của AB không ? Vì sao...

Đọc tiếp

#Toán lớp 6

2

NA

Nguyễn acc 2

13 tháng 3 2022

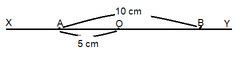
undefined

a. điểm O nằm giữa 2 điểm còn lại

b. ta có : OA + OB = AB

hay 5 + OB = 10

OB = 10 - 5 = 5(cm)

c. vì \(OA=OB=\dfrac{AB}{2}=5\left(cm\right)\)

nên O là trung điểm AB

Đúng(1)

TC

TRẦN CÔNG THỊNH PHÚ

13 tháng 3 2022

HELP ME!!!

Đúng(0)

TT

Trần Trung Đức

5 tháng 9 2019 - olm

Cho góc nhọn xOy. Điểm M nằm trong góc xOy. Tìm trên Ox 1 điểm A, Oy 1 điểm B sao cho điểm A đối xứng với B qua M.

Mn giúp mình nhé <3

#Toán lớp 8

1

D

Darlingg🥝

5 tháng 9 2019

Gọi điểm M trong góc sẽ đặt ra ngoài

Xét tia M bất kì ABC có B và C lần lượt nằm trên hai tia Ox và Oy.

Gọi M’ và M” là các điểm đối xứng với điểm xOy lần lượt qua các đường thẳng Ox và Oy.

Gọi M là của điểm chung của góc nhọn ta có : \(M=xOy+Oy+M+AB+BC\)

Dấu “=” xảy ra khi bốn điểm A′,B,C,A”A′,B,C,A” thẳng hàng.

Suy ra để tính đc đối điểm thì phải lấy B và C lần lượt là giao điểm của đoạn thẳng A’A” với hai tia Ox và Oy (các giao điểm đó tồn tại vì góc xOy nhọn)

Còn lại chịu

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP